A small filament is at the centre of a hollow glass sphere of inner and outer radii 8 cm and 9 cm respectively. The refractive index of glass is 1.50. Calculate the position of the image of the filament when viewed from outside the sphere.
For refraction at the first surface, μ1=1,μ2=1.50,u=−8cm
R = -8cm
μ2v−μ1u=μ2−μ1R
1.5v.−100−8cm=1.50−1.00−8cm
v = -8 cm
It means that due to the first surface the image is formed at the centre of the sphere. For the second surface, μ1=1.50,μ2=1,u=−9cm,R=−9cm
μ2v−μ1u=μ2−μ1R
1v=1.50−9cm=1−1.50−8cm
v = -9 cm
Hence, the final image is formed at the centre of the sphere.

Similar Questions
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Calculate the height of the cone.
View SolutionA hollow spherical body of inner and outer radii 6 cm, and 8 cm respectively floats half submerged in water. Find the density of the material of the sphere.
View Solution
Knowledge Check
The radii of curvature of the two surface of a double convex glass lens are 10 cm and 20 cm respectively. If the refractive index of glass in 1.5, then its focal length will be
A8.5 cmB13.33 cmC20.7 cmD25.2 cmThere is a small air bubble at the centre of a solid glass sphere of radius 'r' and refractive index μ. What wil be the apparent distance of the bubble from the centre of the sphere, when viewed from outside?
ArBrμCr(1−1μ)DZeroAn air bubble in sphere having 4cm diameter appears of 1 cm from surface nearest to eye when looked along diameter. If nga = 1.5, the distance of bubble from refracting surface is
A1.2 cmB3.2 cmC2.8 cmD1.6 cm
A hollow sphere of internal and external radii 6 cm and 8 cm respectively, is melted and recast into small cones of base radius 2 cm and height 8 cm.Find the number of cones.
View SolutionCalculate the focal length of a biconvex lens in air if the radii of its surfaces are 60 cm and 15 cm. Refractive index of glass = 1.5
View SolutionA small air bubble in a glass sphere of radius 2cm appears to be 1cm from the surface when looked at, along a diameter. If the refractive index of glass is 1.5, find the true position of the air bubble.
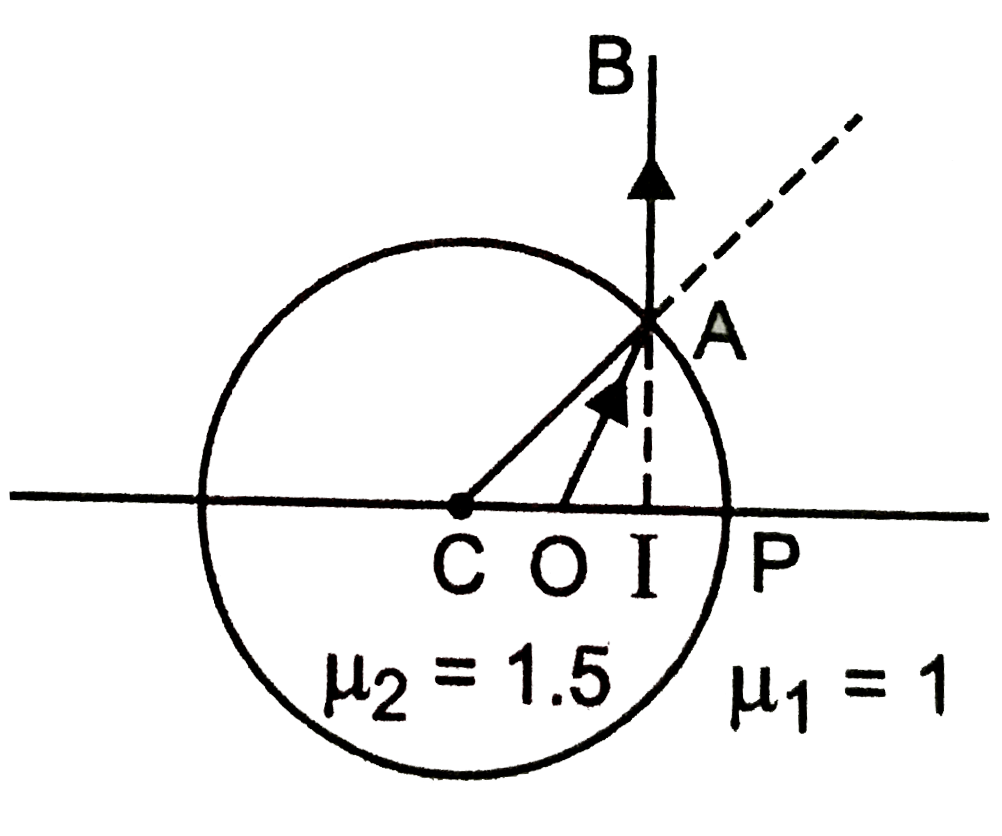 .
.
View SolutionThe radius of a glass ball is 5 cm. There is an air bubble at 1cm from the centre of the ball and refractive index of glass is 1.5. The position of image viewed from surface near the bubble is.
View SolutionA mark is made on the surface of a glass sphere of diameter 10 cm and refractive index 1.5. It is viewed through the glass from a portion directly opposite. The distance of the image of the mark from the centre of the sphere will be
View Solution
