Prove that the average pressure of a liquid (density p) on the walls of the container filled upto height h with liquid is 12hρg.
To prove that the average pressure of a liquid (density ρ) on the walls of a container filled up to height h with the liquid is given by 12ρgh, we can follow these steps:
Step 1: Understand the Pressure at a Depth
The pressure at a depth y in a liquid is given by the formula:
P=ρgy
where:
- P is the pressure,
- ρ is the density of the liquid,
- g is the acceleration due to gravity,
- y is the depth from the surface of the liquid.
Step 2: Consider a Differential Element
Consider a small horizontal strip of the wall of the container at a depth y with thickness dy. The area of this strip is:
dA=2πrdy
where r is the radius of the container.
Step 3: Calculate the Force on the Differential Element
The force dF exerted by the liquid on this differential area dA due to pressure is:
dF=P⋅dA=ρgy⋅(2πrdy)
Thus,
dF=2πrρgydy
Step 4: Integrate to Find Total Force
To find the total force F on the walls of the container, we integrate dF from y=0 to y=h:
F=∫h0dF=∫h02πrρgydy
Calculating the integral:
F=2πrρg∫h0ydy=2πrρg(y22)h0=2πrρg⋅h22
Thus, we have:
F=πrρgh2
Step 5: Calculate the Total Area of the Walls
The total curved surface area A of the container is:
A=2πrh
Step 6: Calculate the Average Pressure
The average pressure Pavg on the walls is given by the total force divided by the total area:
Pavg=FA=πrρgh22πrh
Simplifying this expression:
Pavg=ρgh22h=12ρgh
Conclusion
We have shown that the average pressure of a liquid on the walls of the container is:
Pavg=12ρgh
The pressure at a depth y in a liquid is given by the formula:
P=ρgy
where:
- P is the pressure,
- ρ is the density of the liquid,
- g is the acceleration due to gravity,
- y is the depth from the surface of the liquid.
Consider a small horizontal strip of the wall of the container at a depth y with thickness dy. The area of this strip is:
dA=2πrdy
where r is the radius of the container.
The force dF exerted by the liquid on this differential area dA due to pressure is:
dF=P⋅dA=ρgy⋅(2πrdy)
Thus,
dF=2πrρgydy
To find the total force F on the walls of the container, we integrate dF from y=0 to y=h:
F=∫h0dF=∫h02πrρgydy
Calculating the integral:
F=2πrρg∫h0ydy=2πrρg(y22)h0=2πrρg⋅h22
Thus, we have:
F=πrρgh2
The total curved surface area A of the container is:
A=2πrh
The average pressure Pavg on the walls is given by the total force divided by the total area:
Pavg=FA=πrρgh22πrh
Simplifying this expression:
Pavg=ρgh22h=12ρgh
We have shown that the average pressure of a liquid on the walls of the container is:
Pavg=12ρgh
Similar Questions
Knowledge Check
A tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
 A2√h(H−h)B√h(H−h)C2√h2H−hD√h2H−h
A2√h(H−h)B√h(H−h)C2√h2H−hD√h2H−h
In the arrangement shown two liquids of density ρ and 2ρ are filled in a container the height of both liquids is h. there are two holes A and B at heights h1 and h2 from top liquid surface and bottom of the vessel. if V1 and V2 are the velocities of efflux at the two holes A and B respectively, find the correct graph.
Take =α(V2V1)2A B
B C
C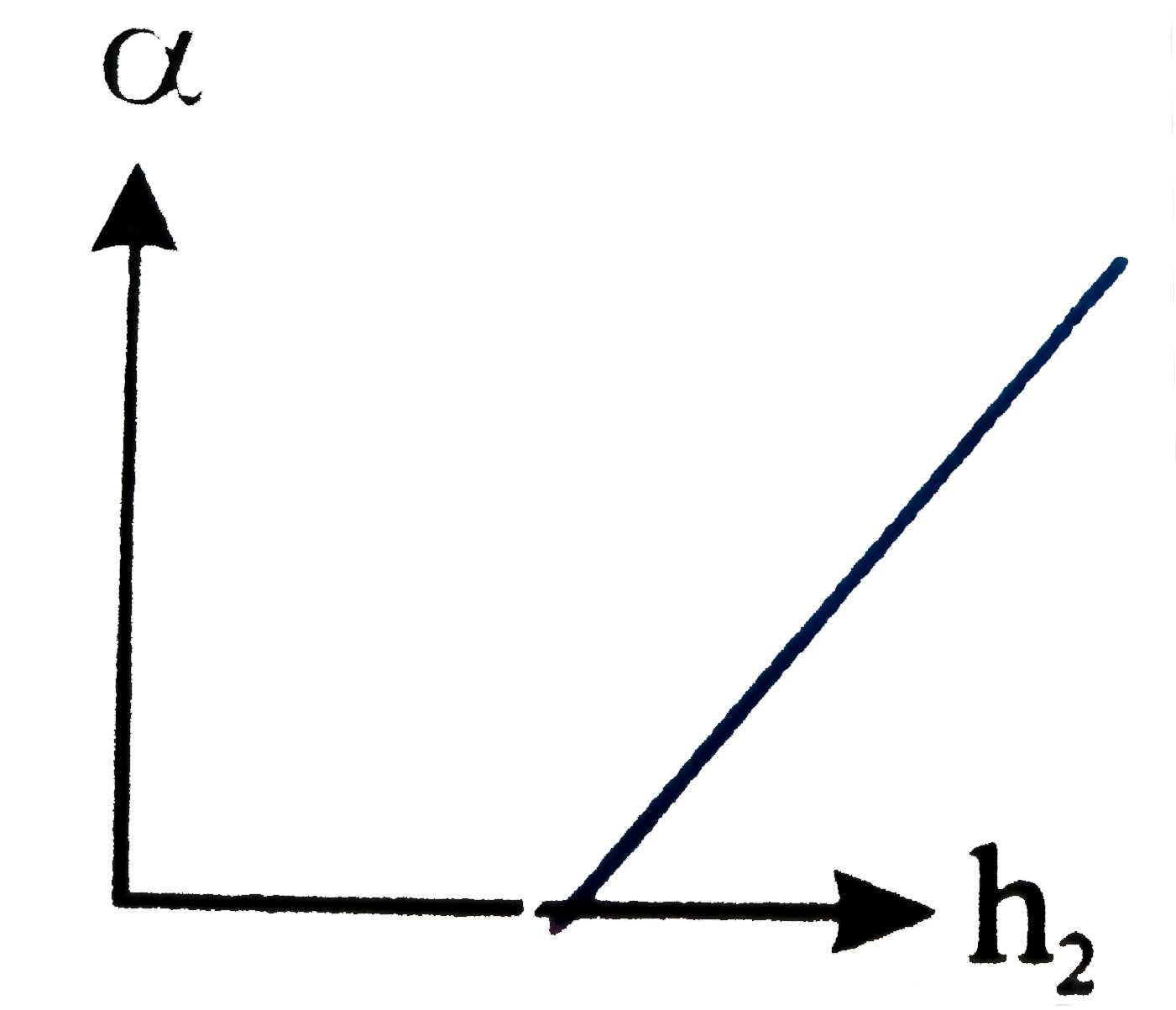 D
D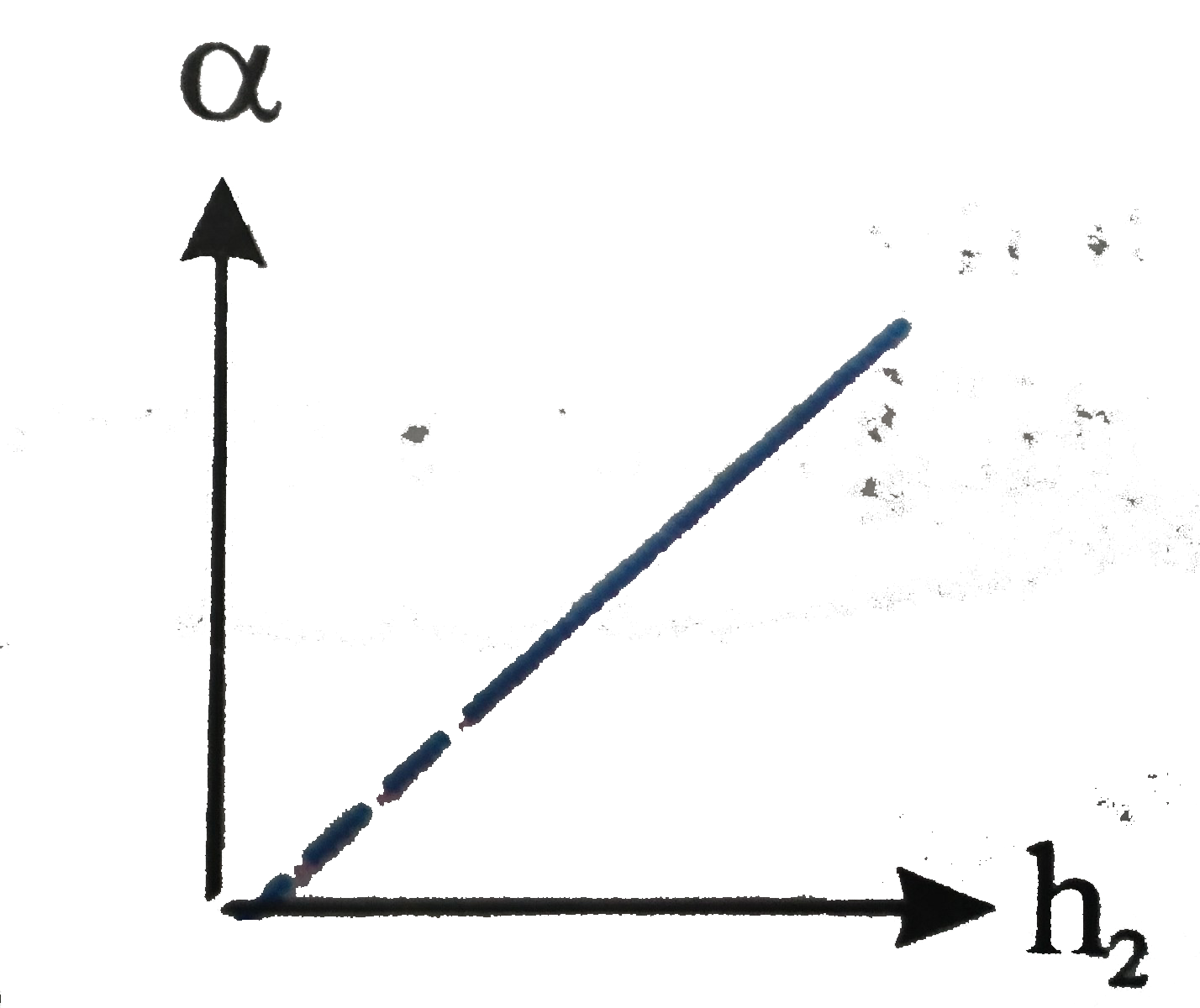
A cylindrical vessel of radius r is filled with a homogeneous liquid upto a height h. It is found that the force exerted by the liquid column on the bottom of the cylinder is equal to the force exerted by the liquid on the sides of the cylinder. What is the relation between r and h?
Ar=h2Br=hCr=2hDr=32h
The net presseure acting at the bottom of a container filled with a liquid of density 'd' to a height of h is hdg.
View SolutionTwo identical cylindrical vessels with their bases at the same level each, contain a liquid of density ρ. The area of either base is A but in one vessel the liquid height is h1 and in the other liquid height is h2(h2<h1). If the two vessel are connected, the work done by gravity in equalizing the level is
View SolutionLiquid of density ρ in a container exerts pressure P given by (height of liquid h and area A)
View SolutionThe pressure exerted by a liquid of height h is given by(symbols have their usuall meanings)
View SolutionThe pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
View Solution
