You are supplied with a number of 100Ω resistors. How could you combine some of these resistors to make a 250Ω resistor?
The correct Answer is:Combine two 100Ω resistors in series with a parallel combination of two 100Ω resistors
To create a 250Ω resistor using 100Ω resistors, we can follow these steps:
Step 1: Connect Two Resistors in Series
First, take two 100Ω resistors and connect them in series. The total resistance of resistors in series is simply the sum of their resistances.
\(
R_{series} = R_1 + R_2 = 100 Ω + 100 Ω = 200 Ω
\)
Step 2: Connect Two Resistors in Parallel
Next, take another two 100Ω resistors and connect them in parallel. The formula for the equivalent resistance \( R_{parallel} \) of two resistors in parallel is given by:
\(
\frac{1}{R_{parallel}} = \frac{1}{R_1} + \frac{1}{R_2}
\)
Substituting the values:
\(
\frac{1}{R_{parallel}} = \frac{1}{100 Ω} + \frac{1}{100 Ω} = \frac{2}{100 Ω}
\)
Now, solving for \( R_{parallel} \):
\(
R_{parallel} = \frac{100 Ω}{2} = 50 Ω
\)
Step 3: Combine the Two Sets in Series
Now, take the equivalent resistance from the first step (200 Ω) and the equivalent resistance from the second step (50 Ω) and connect them in series:
\(
R_{total} = R_{series} + R_{parallel} = 200 Ω + 50 Ω = 250 Ω
\)
Conclusion
Thus, by connecting two 100Ω resistors in series to get 200Ω and two 100Ω resistors in parallel to get 50Ω, and then combining these two results in series, we achieve a total resistance of 250Ω.
---
First, take two 100Ω resistors and connect them in series. The total resistance of resistors in series is simply the sum of their resistances.
R_{series} = R_1 + R_2 = 100 Ω + 100 Ω = 200 Ω
\)
Next, take another two 100Ω resistors and connect them in parallel. The formula for the equivalent resistance \( R_{parallel} \) of two resistors in parallel is given by:
\frac{1}{R_{parallel}} = \frac{1}{R_1} + \frac{1}{R_2}
\)
\frac{1}{R_{parallel}} = \frac{1}{100 Ω} + \frac{1}{100 Ω} = \frac{2}{100 Ω}
\)
R_{parallel} = \frac{100 Ω}{2} = 50 Ω
\)
Now, take the equivalent resistance from the first step (200 Ω) and the equivalent resistance from the second step (50 Ω) and connect them in series:
R_{total} = R_{series} + R_{parallel} = 200 Ω + 50 Ω = 250 Ω
\)
Thus, by connecting two 100Ω resistors in series to get 200Ω and two 100Ω resistors in parallel to get 50Ω, and then combining these two results in series, we achieve a total resistance of 250Ω.
Topper's Solved these Questions
- ELECTRICITY BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - ELECTRICITY EXERCISE - Very Short Answer Type Questions
1 Videos
- ELECTRICITY BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - ELECTRICITY EXERCISE - Short Answer Type Questions
2 Videos
- ELECTRICITY BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - ELECTRICITY EXERCISE - Sample Problem
1 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - NCERT BOOK
2 Videos
Similar Questions
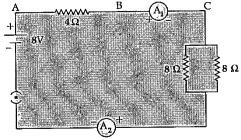
Power dissipated in 4Ω resistor is :
View SolutionRahul went to an electronics shop to get his father's old radio set repaired. The radio mechanic required resistances of 1.5Ω and 10Ω to repair the radio set properly but he had only a large number of 3Ω resistors. The radio mechanic made many attempts but could not get the right combinations of 3Ω resistors to obtain 1.5Ω and 10Ω resistances. Rahul had studied combination of resistors in class X. Rahul thought for a while and then joined some 3Ω resistors in two different ways to obtain the required resistances.
(a) How did Rahul obtain 1.5Ω resistance by joining a number of 3Ω resistors ?
(b) How many 3Ω resistors were combined together to obtain 1.5Ω resistance ?
(c) How did Rahul obtain 10Ω resistance by joining a number of 3Ω resistors ?
(d) How many 3Ω resistors were combined together by Rahul to obtain 10Ω resistance ?
(e) What values are shown by Rahul in this apisode ?
View Solution
Knowledge Check
Current through the 5Ω resistor is
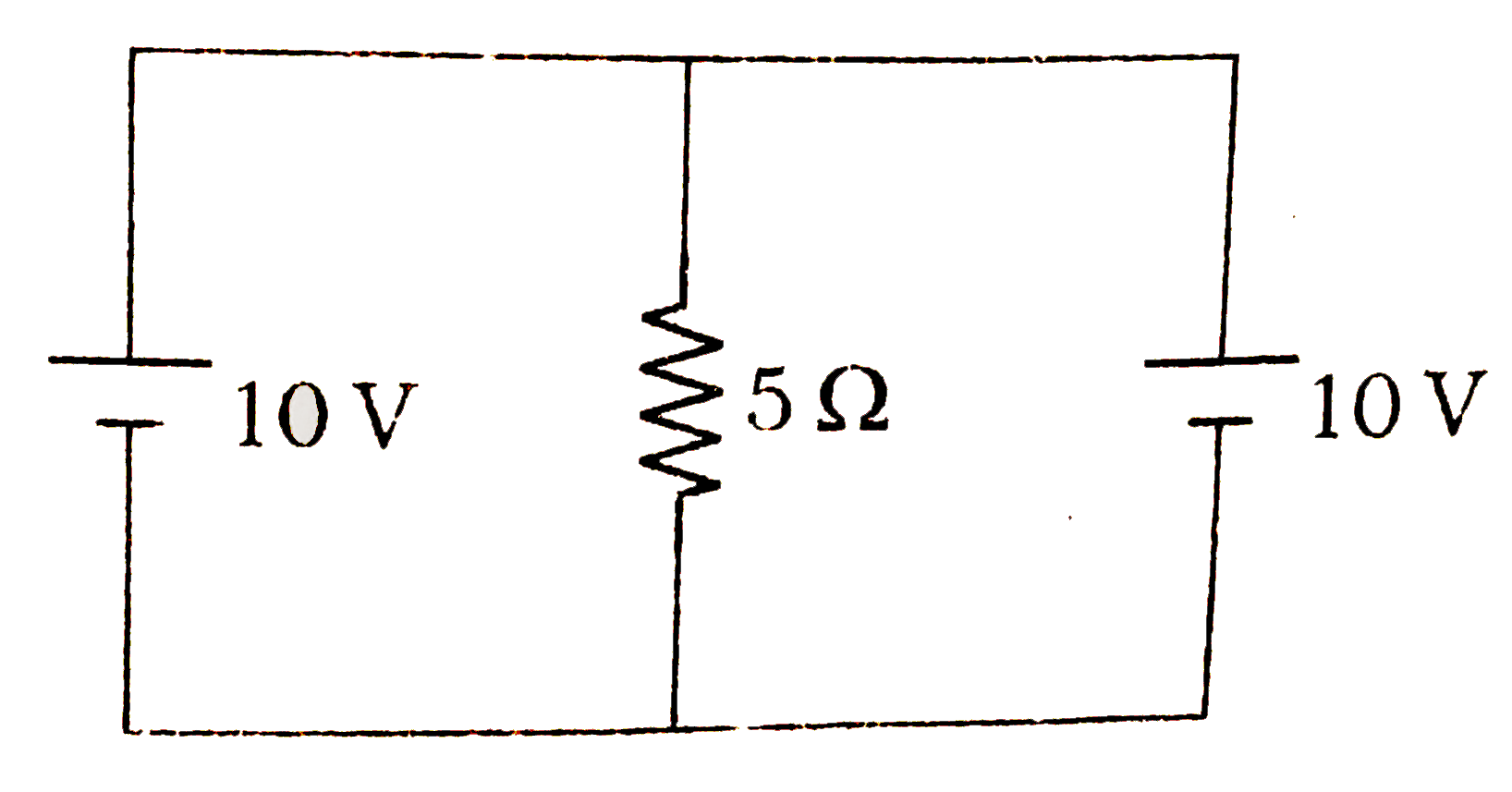 A2AB4ACzeroD1A
A2AB4ACzeroD1AThe power dissipated 6Ω resistor is
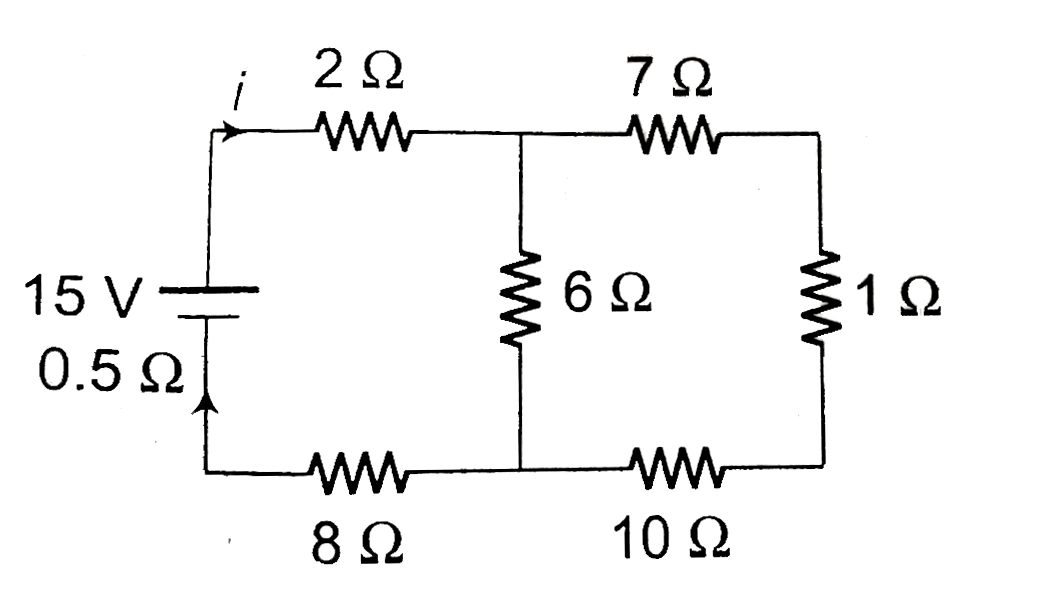 A278WB916WC616WD316W
A278WB916WC616WD316WIf power dissipated in the 9Ω resistor in the resistor shown is 36W, the potential difference across the 2Ω resistor is
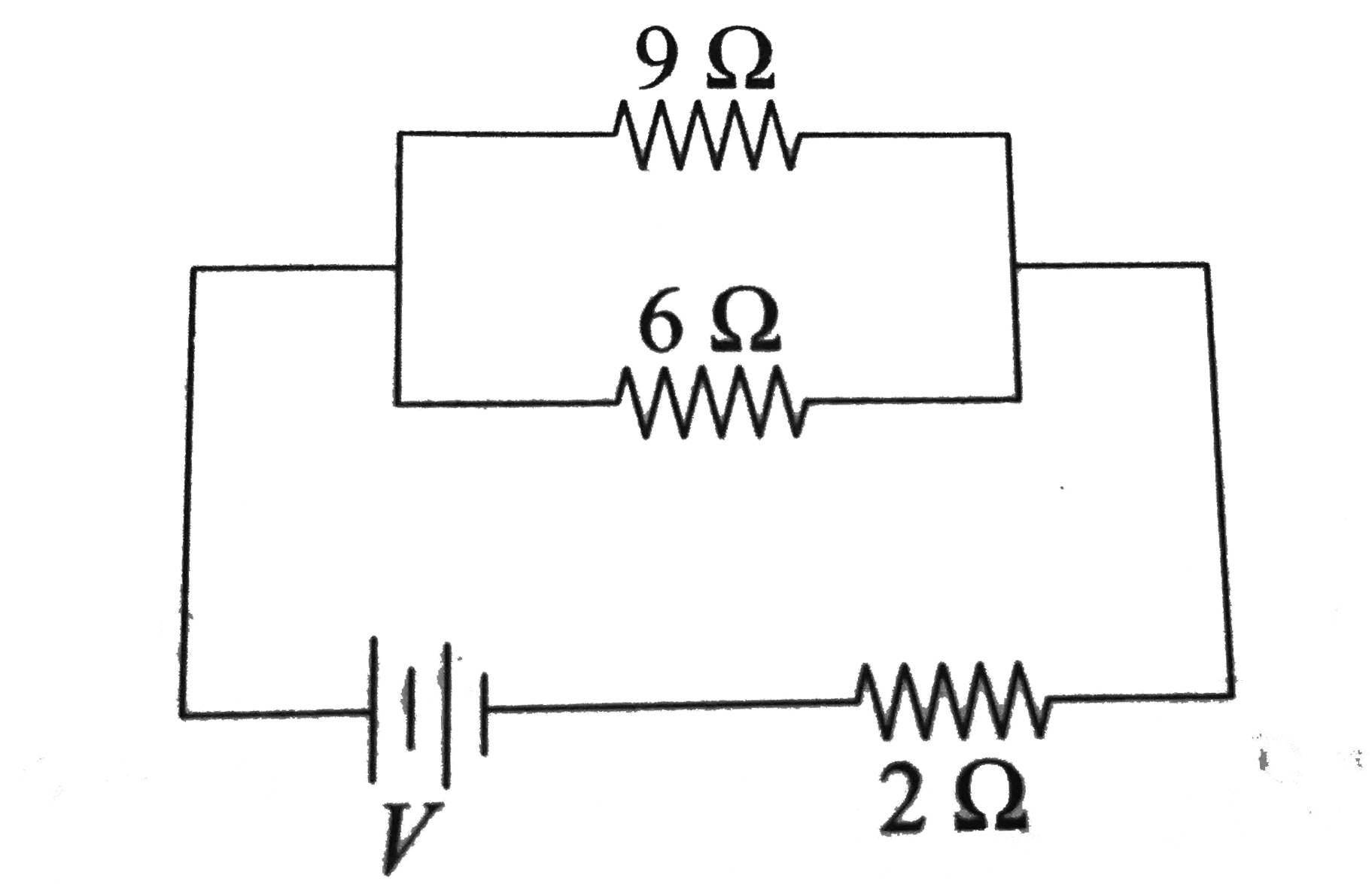 A8VB10VC2VD4V
A8VB10VC2VD4V
A resistor of 5Ω is connected in series with a parallel combination of a number of resistors each of 5Ω. If the total resistance of the combination is 6Ω , how many resistor are in parallel?
View SolutionGiven three resistors of resistances 1Ω,2Ωand3Ω. How will you combine them to get an equivalent resistance of 115Ω ?
View SolutionDraw a schematic diagram of a circuit consisting of a battery of three cells of 2V each, a 5Ω resistor , and 8Ω resistor and a 12Ω resistor and a plug key, all connected in series.
View SolutionCompare the power used in the 2 ω resistor in each of the following circuits :
a 6 V battery in series with 1 ω and 2 ω resistors, and
View Solution6Ω and 12Ω resistors are connected in parallel. This combination is connected in series with 10 V battery and 6Ω resistor. What is the potential differnce between the terminals of the 12Ω resistor ?
View Solution
