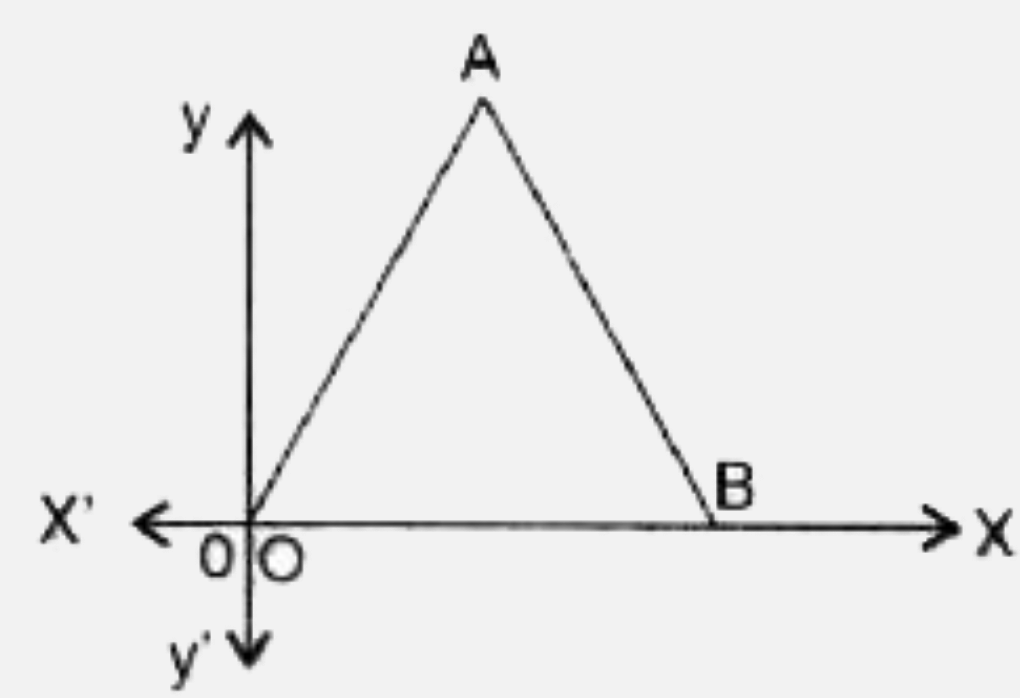
In the figure given below. ABC is an equilateral triangle. Find the co-ordinates of the vertices.
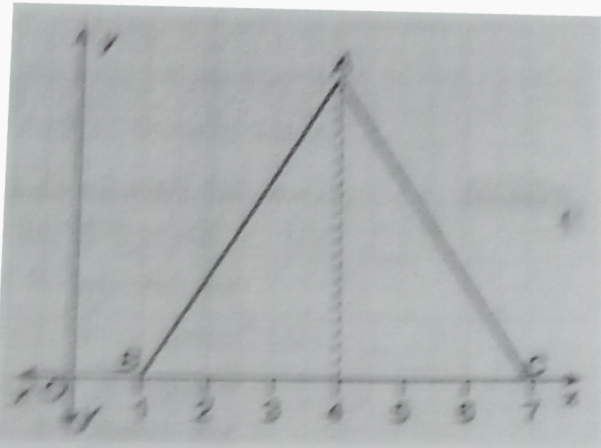
Text Solution
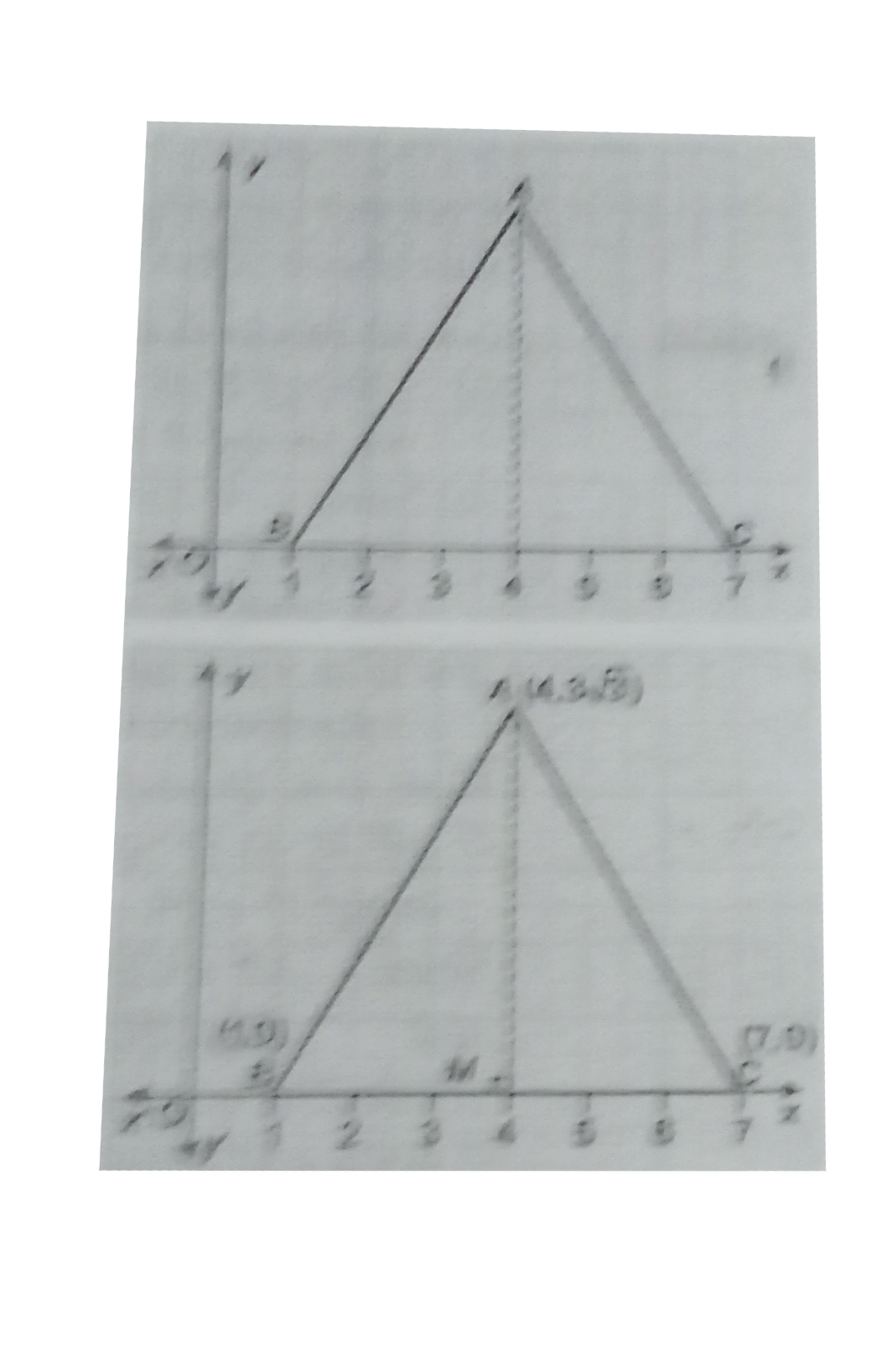
From the figure, BC=6 units.
As ABC is an equilateral triangle, AB=BC=6 units. From A, draw AM⊥BC, then M is the mid-point of BC.
So, BM=12BC
12×6 units=3units.
In ΔABM, ∠M=90∘. By the Pythagoras theorem, we get
AB2=AM2+BM2
⇒62−AM2+32
⇒AM2=36−9=27
⇒AM=√3 units.
From figure, OM=OB+BM=(1+3) units =4 units. Clearly, co-ordinates of B and C are (1,0) and (7,0) respectively.
As AM=3√3 units and OM=4 units, therefore, co-ordinates of A are (4,3√3).
|
Topper's Solved these Questions
- CO-ORDINATE GEOMETRY Book:NAGEEN PRAKASHANChapter:CO-ORDINATE GEOMETRY Exercise:Problems From NCERT/ Exemplar
Explore 6 Videos
- CO-ORDINATE GEOMETRY Book:NAGEEN PRAKASHANChapter:CO-ORDINATE GEOMETRY Exercise:Revision Exercise
Explore 8 Videos
- CIRCLE Book:NAGEEN PRAKASHANChapter:CIRCLE Exercise:Revision Exercise (long Answer Questions )
Explore 5 Videos
- CONSTRUCTIONSBook:NAGEEN PRAKASHANChapter:CONSTRUCTIONSExercise:EXAMPLE SOLUTION.
Explore 19 Videos
Similar Questions
Knowledge Check
In the given figure, ΔABC is an equilateral triangle. Find ∠BEC :
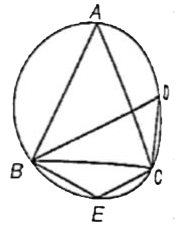 A120∘B60∘C80∘Dnone of the above
A120∘B60∘C80∘Dnone of the aboveIn the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.
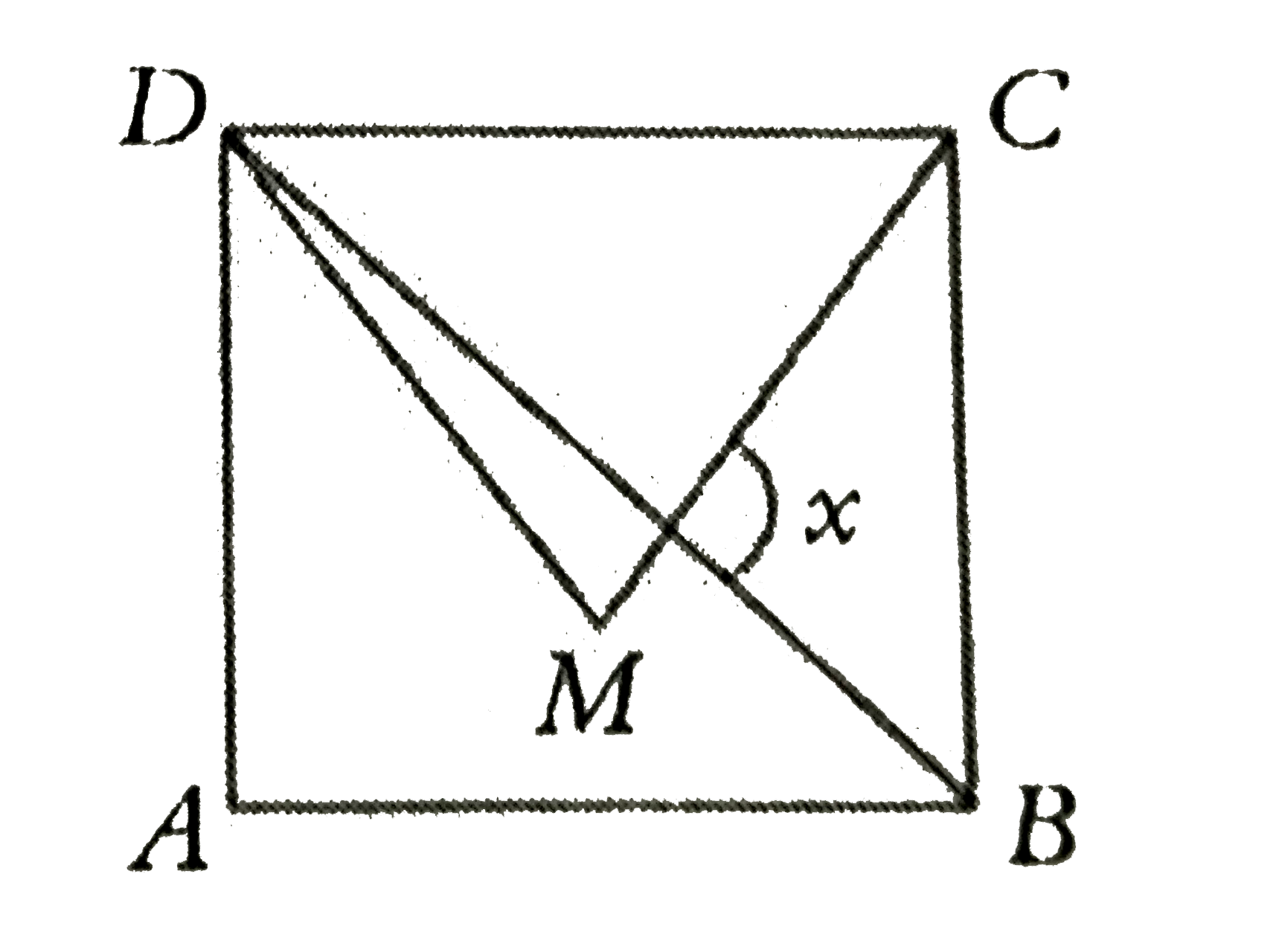 A75∘B90∘C105∘D60∘
A75∘B90∘C105∘D60∘
In Figure, ABC is an equilateral triangle. Find m ∠BEC
View SolutionIn the given figure, ΔABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices.
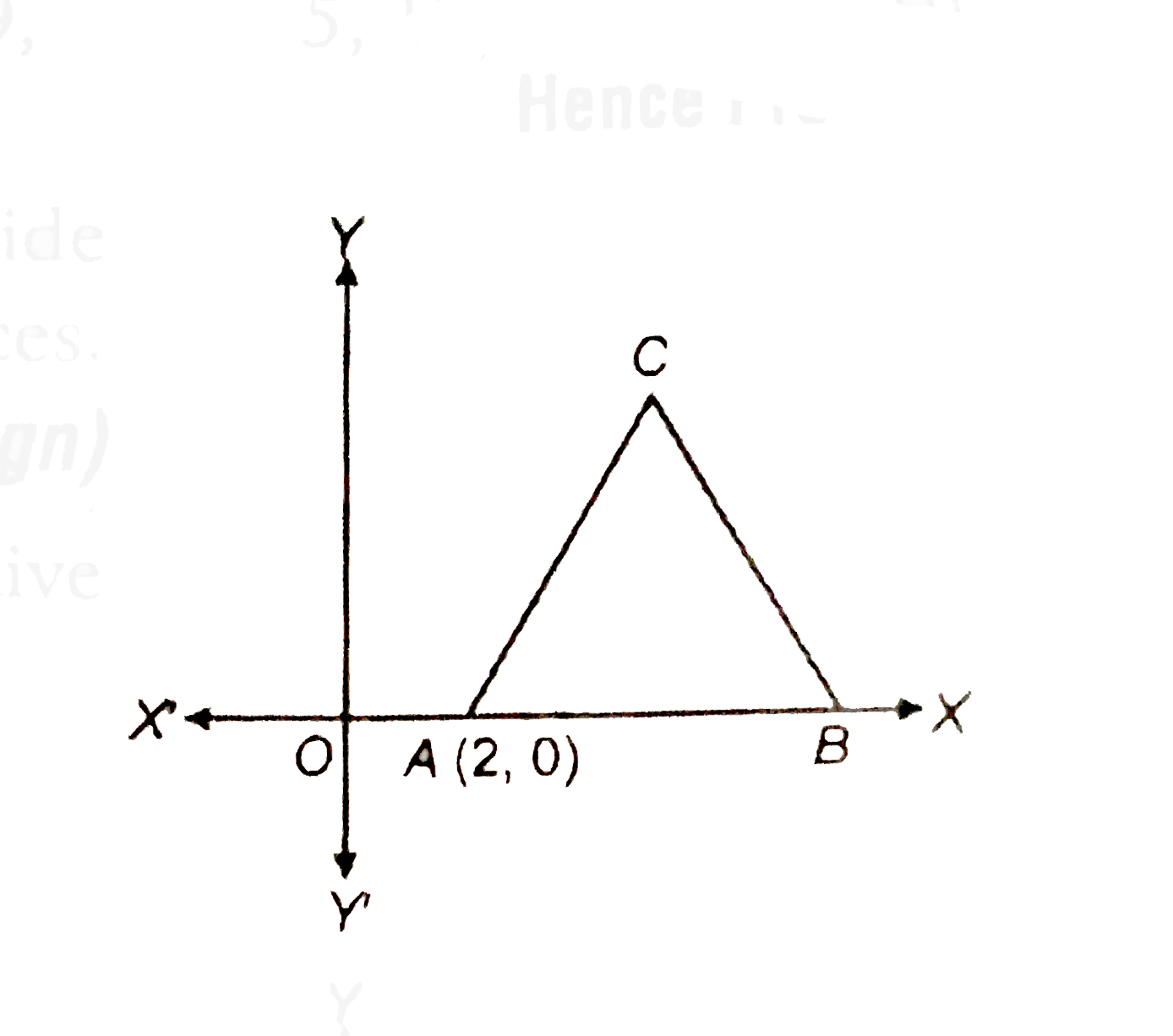
View SolutionIn the given figure, ΔABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices.
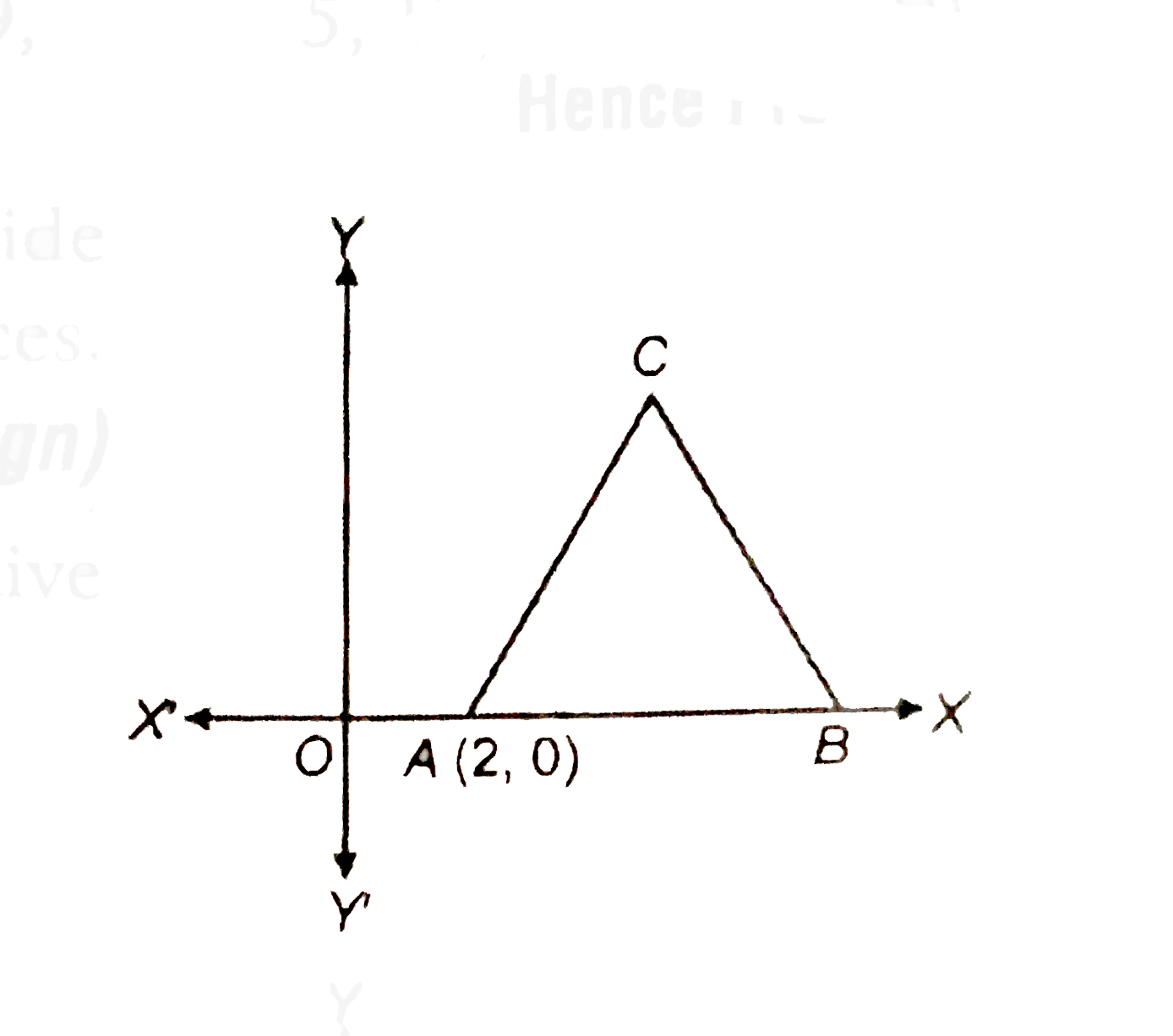
View SolutionIn the figure given below, ABC is an equilateral triangle.D, E, F, G, H and I are the trisector points of the sidesas shown. If the side of the triangle ABC is 6 cm, then the area of the regular hexagon DEFGHI is
View SolutionIn the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.

View SolutionIn Figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC
View Solution