A regular hexagone of side a. A wire of length 24 a is coiled on that hexagone. If current in hexagone is I, then find the magnetic moment.
6√3la2
3√3la2
3√32la2
6la2
The correct Answer is:A
Let number of turns = n
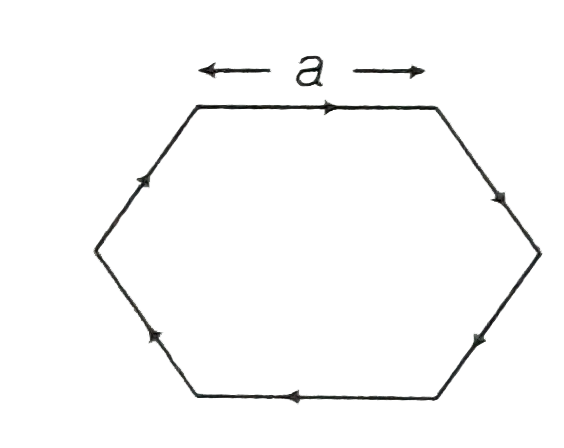
∴n=4
Magnetic moment, M=nIA = 4IA
∴ Area of hexagone = 12a2sin60∘+a.2asin60∘+12a2sin120∘
=√34a2+√3a2+√3a24
=6√3a24=3√3a22
Hence, magnetic moment = 4I3√3a22=6√3Ia2
Topper's Solved these Questions
- SOLVED PAPERS 2018BOOK - DC PANDEYCHAPTER - SOLVED PAPERS 2018EXERCISE - Assertion and Reasons
10 Videos
- SOLVED PAPER 2017BOOK - DC PANDEYCHAPTER - SOLVED PAPER 2017EXERCISE - Solved papers 2017(JIPMER)
32 Videos
- WAVE OPTICSBOOK - DC PANDEYCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced E. Integer Type Questions
13 Videos
Similar Questions
A uniform conducting wire of length 18a and resistance R is wound up as current carrying coil in the shape of a regular a hexagon of sides a. If the coil is connected to a voltage source V0, then the magnetic moment of coil is

View SolutionThe circumference of a circle is 128 m. What is the area of the circle ?
View Solution
Knowledge Check
Area of regular hexagon with side 'a' is
A3√34a2 sq. unitB122√3a2 sq. unitC92√3a2 sq. unitD6√2a2 sq. unitSix s imilar magnetic poles are placed on six corners of a regular hexagon of side 10cm. A south pole of strength 10Am is placed at the centre of hexagon. Find the magnetic force on the south pole.
AZeroB4π×10−4NC10 NDNone of theseArea of a regular hexagon with side ‘a’ is
A3√34a2 sq. unitB122√3a2 sq. unitC92√3a2 sq. unitD6√2a2 sq. unit
The area of a regular hexagon of side 2√3 cm is :
View SolutionA regular hexagon of side a has a charge Q at each vertex. Potential at the centres of hexagon is (k= (14πε0))
View SolutionEach angle of a regular hexagon is:
View SolutionA regular hexagon is inscirbed in a circle of radius R . Another circle is inscribed in the hexagon . Now another hexagon is inscribed in the second ( smaller ) circle .
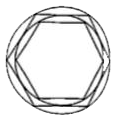
If thre are some more circle and hexagons inscribed in the similar way as given above, then the ratio of each side of outermost hexagon ( largest one ) to that of the fourth ( smaller cone ) hexagon is ( fourth hexagon means the hexagon which is inside the third hexagon from the outside ):
View SolutionThe area of a regular hexagon of side 2√3 cm is :
View Solution
