Positive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x $< <$ R, find the time period of oscillation of the particle if it is released from there.

A

${[\frac{16 π^{3} ε_{0} R^{3} m}{Q q}]}^{1 / 2}$

B

${[\frac{8 π^{2} ε_{0} R^{3}}{q}]}^{\frac{1}{2}}$

C

${[\frac{2 π^{3} ε R^{3}}{3 q}]}^{1 / 2}$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

When the negative charge is shifted at a distance x from the center of the ring along its axis, then force acting on the point charge due to the ring.

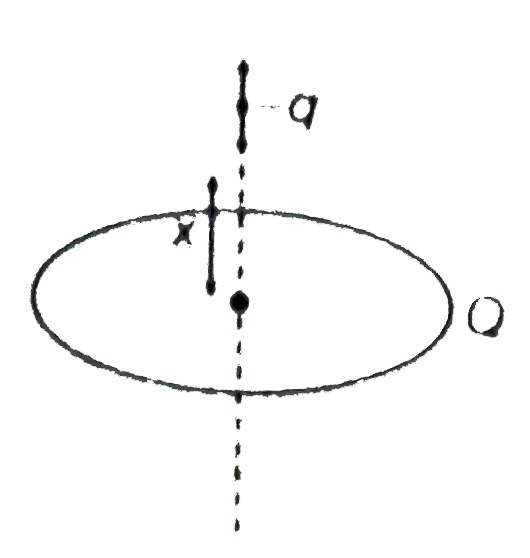
F=qE(towards center)
$= q . \frac{k O x}{{(R^{2} + x^{2})}^{3 / 2}}$
If Rgtgtx, then $R^{2} + x^{2} \approx R^{2}$
and $F = \frac{1}{4 π ε_{0}} . \frac{Q q x}{R^{3}}$ (towards centre)
$\Rightarrow a = \frac{F}{m} = \frac{1}{4 π ε_{0} . \frac{Q q x}{m R^{3}}}$
Since, restoring force $F_{E} \propto x$ , therefore motion of charge particle will be SHM.
Time period of SHM,
$T = \frac{2 π}{ω} = {[\frac{16 π^{3} ε_{0} R^{3} m}{Q q}]}^{\frac{1}{2}}$ $[∴ ω^{2} = \frac{Q q}{4 π ε_{0} R^{3}}]$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A positive charge $Q$ is uniformly distrubuted along a circular ring of radius $R$ .a small test chage $q$ is placed at the centre of the ring .The

Aif $q > 0$ and is displaced away from the centre in the plane of the ring.it will be pushed back towards the centre.
Bif $q < 0$ and is displaced away from the cnetre in the plane of the ring .it will never return to the centre and will continue moving till it hits the ring.
Cif $q < 0$ it will perform $S H M$ for small displacement along the axis
D $q$ at the centre of the ring is in an unstable equilibrium within the plane of the ring for $q < 0$
Question 2 - Select One
A long straight wire carries a charge with linear density $λ$ . A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
A $\sqrt{\frac{q λ ln r}{π m \in_{0}}}$
B $\sqrt{\frac{q λ ln 2}{π m \in_{0}}}$
C $\sqrt{\frac{q λ ln 2}{2 π m \in_{0}}}$
D $\sqrt{\frac{q λ ln 2}{π m \in_{0}}}$
Question 3 - Select One
A ring of radius R is charged uniformly with a charge $+ Q$ . The potential at a point on its axis at a distance 'r' from any point on ring will be-
A $\frac{k Q}{\sqrt{R^{2} + r^{2}}}$
B $\frac{k Q}{r}$
C $\frac{k Q}{{(r^{2} + R^{2})}^{3 / 2}}$
D $\frac{k Q}{r^{2}} {(r^{2} - R^{2})}^{1 / 2}$

DC PANDEY-SOLVED PAPERS 2018-AIIMS

Home
Ask Doubt
Profile