A simple pendulum consists of a small sphere of mass m suspended by a thread of length l. the sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically upwards. With what period will pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force ?
The two forces acting on the bob are shown in figure
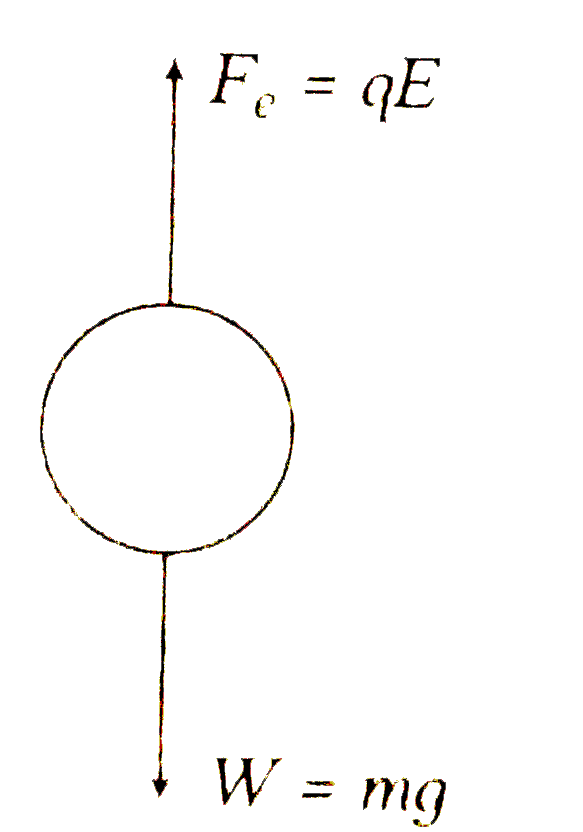
geff in this case will be W−Fem
or geff=mg−qEm=g−qEm
∴T=2π√lgeff=2π
⎷lg−qEm
Similar Questions
A simple pendulum consists of a small sphere of mass m suspended by a thread of length l. The sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically downwards. Finds the period of oscillation of the pendulum due to the electrostatic force acting on the sphere, neglecting the effect of the gravitational force.
View SolutionA sphere of mass "50gm" is suspended by a string in an electric field of intensity 5NC1acting vertically upward.If the tension in the string is "520 millinewton,the charge on the sphere is "(g=10ms−2)]
View Solution
Knowledge Check
A Pendulum bob of mass m and charge q is suspended by a thread of length l. The pendulum is placed in a region of a uniform electric field E directed vertically upward. If the electristatic force acting on the sphere is les than that of gravitational fore, calculate the period with which the pendulum oscillates (Assumes small oscillation)
AT=2π ⎷lg+qEmBT=2π ⎷lg−qEmCT=π ⎷lg−qEmDT=π ⎷lg+qEmA simple pendulum of mass m and charge +q is suspended vertically by a massless thread of length l. At the point of suspension, a point charge +q is also fixed. If the pendulum is displaced slightly from equilibrium position, its time period will be
AT=2π ⎷lg+kq2ml2BT=2πCT=2π√lgDwill be greater then 2π√lgA simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.
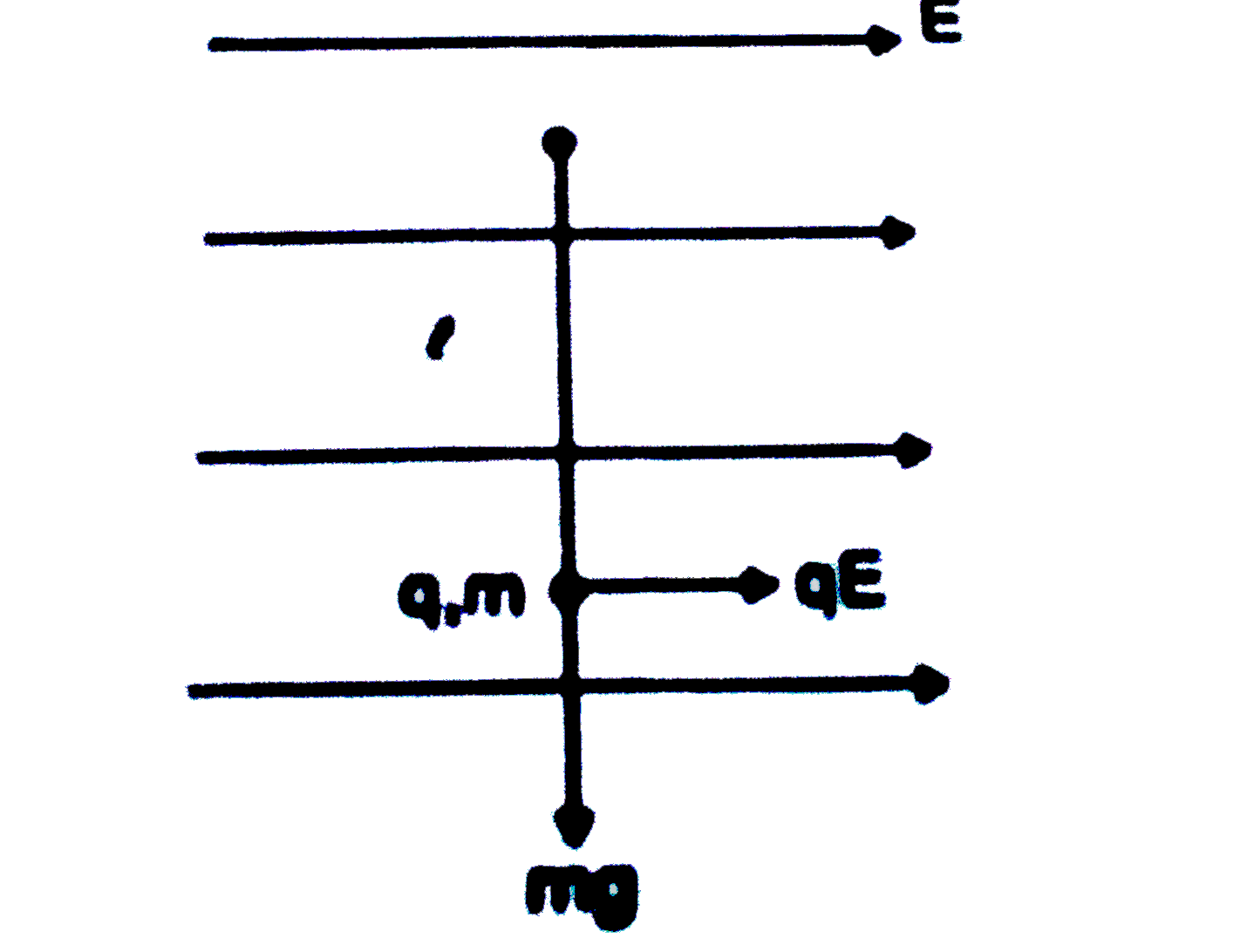 A2π√lgB2π ⎷⎧⎨⎩lg+qEm⎫⎬⎭C2π ⎷⎧⎨⎩lg−qEm⎫⎬⎭D2π ⎷l√g2+(qEm)2
A2π√lgB2π ⎷⎧⎨⎩lg+qEm⎫⎬⎭C2π ⎷⎧⎨⎩lg−qEm⎫⎬⎭D2π ⎷l√g2+(qEm)2
A wagon of mass M can move without friction along horizontal rails. A simple pendulum consisting of a sphere of mass m is suspended from the ceiling of the wagon by a string of length l. At the initial moment the wagon and the pendulum are at rest and the string is deflected through an angle α from the vertical. Find the velocity of the wagon when the pendulum passes through its mean position.
View SolutionIf a simple pendulum has charge q and is oscillating in a uniform electric field E in the direction of acceleration due to gravity, then its frequency of oscillations
View SolutionA uniform electric field →E directed vertically upwards exists in a region of space. A point mass m carrying positive charge q is a state of equilibrium inside this electric field
View SolutionA mass m carrying a charge q si suspended form a string and placed in a uniform horizontal electric field of intensity E.The angel made by the string with the vertical in the equilibrium position is
View SolutionA heavy small sized sphere is suspended by a string of length 2. The sphere is rotated uniformly in a horizontal circle with the string making an angle θwith the vertical. The time period of this conical pendulum is
View Solution
