A mass of 1 kg is acted upon by a single force . Under this force it is displaced from (0,0) to (1m,1m). If initially the speed of the particle was 2 , its final speed should be
The correct Answer is:B
(b) Given, force,
Initial speed,
From work energy theorem we have
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.3
10 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISES(TAKING IT TOGETHER)
83 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.1
20 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
Knowledge Check
A particle is acted upon by only a conservative force F=(7ˆi−6ˆj) N (no other force is acting on the particle). Under the influence of this force particle moves from (0, 0) to (-3m, 4m) then
Awork done by the force is 3 JBwork done by the force is −45JCat (0, 0) speed of the particle must be zeroDat (0, 0) speed of the particle must not be zeroA body of mass 2 kg is acted upon by two forces →D1=(2ˆi+3ˆj)Nand→F2(−2ˆk+3ˆj)N. If the body is displaced from A(3m,−2m,1m) to B (−1m,+2m,−3m), then work done on the body is
A40 JB−40JC24 JD−24JA body is displaced from (0,0) to (1m,1m) along the path x=y by a force F=(x2ˆj+yˆi)N. The work done by this force will be
A43JB56JC32JD75J
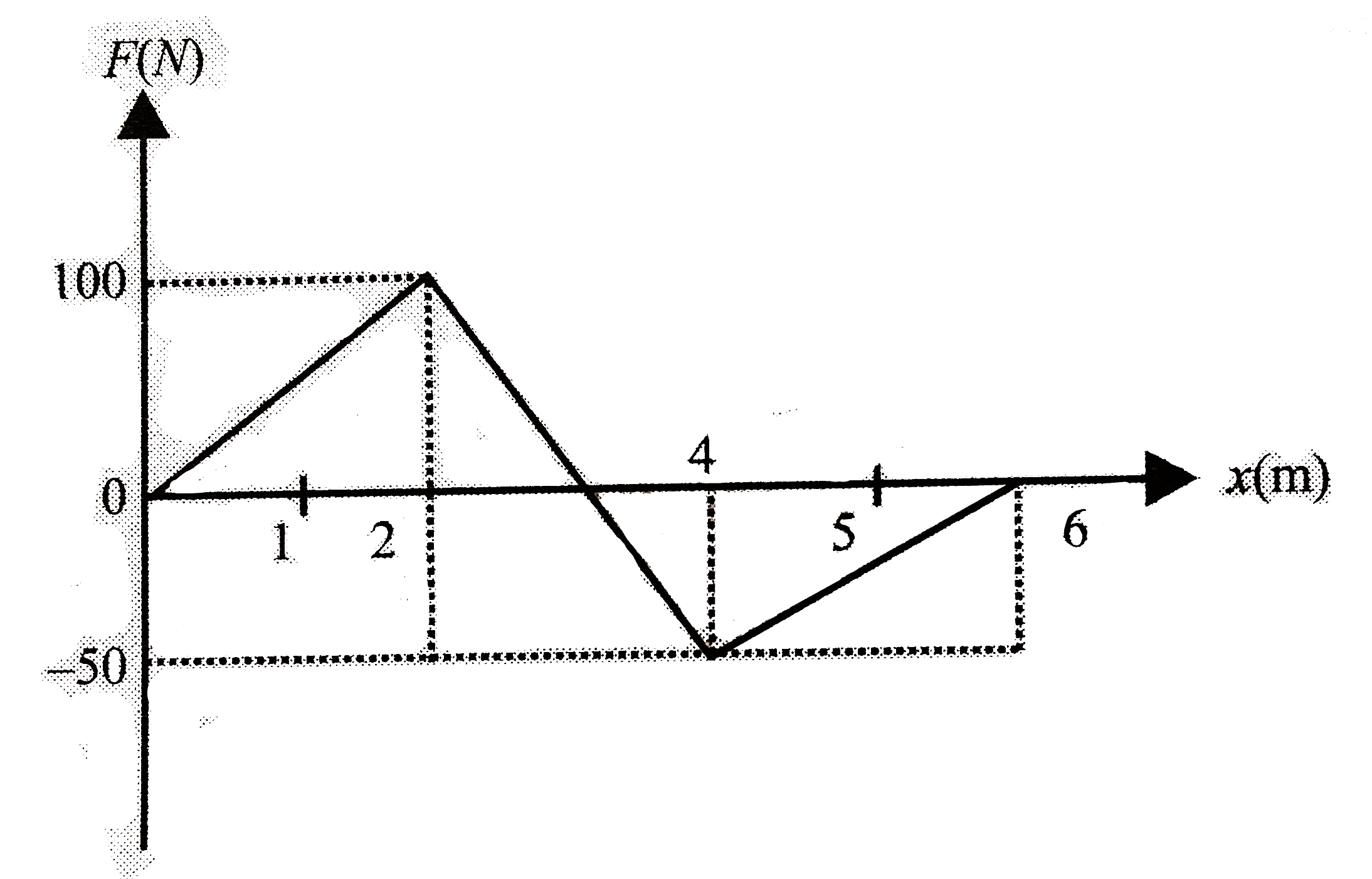
A stationary particle of mass m=1.5kg is acted upon by a variable force. The variation of force with respect to displacement is plotted in figure.
a. Calculate the velocity acquired by the particle after getting displaced through 6m.
b. What is the maximum speed attained by the particle and at what time is it attained?
View SolutionA body of mass 2 kg is acted upon by two forces 2N and 5N in the direction of ˆi+ˆj and ˆj−ˆk respectively. If the body is displaced from (3,-2, 1) to (-1, 2, 3) (Positions are in m), then work done is
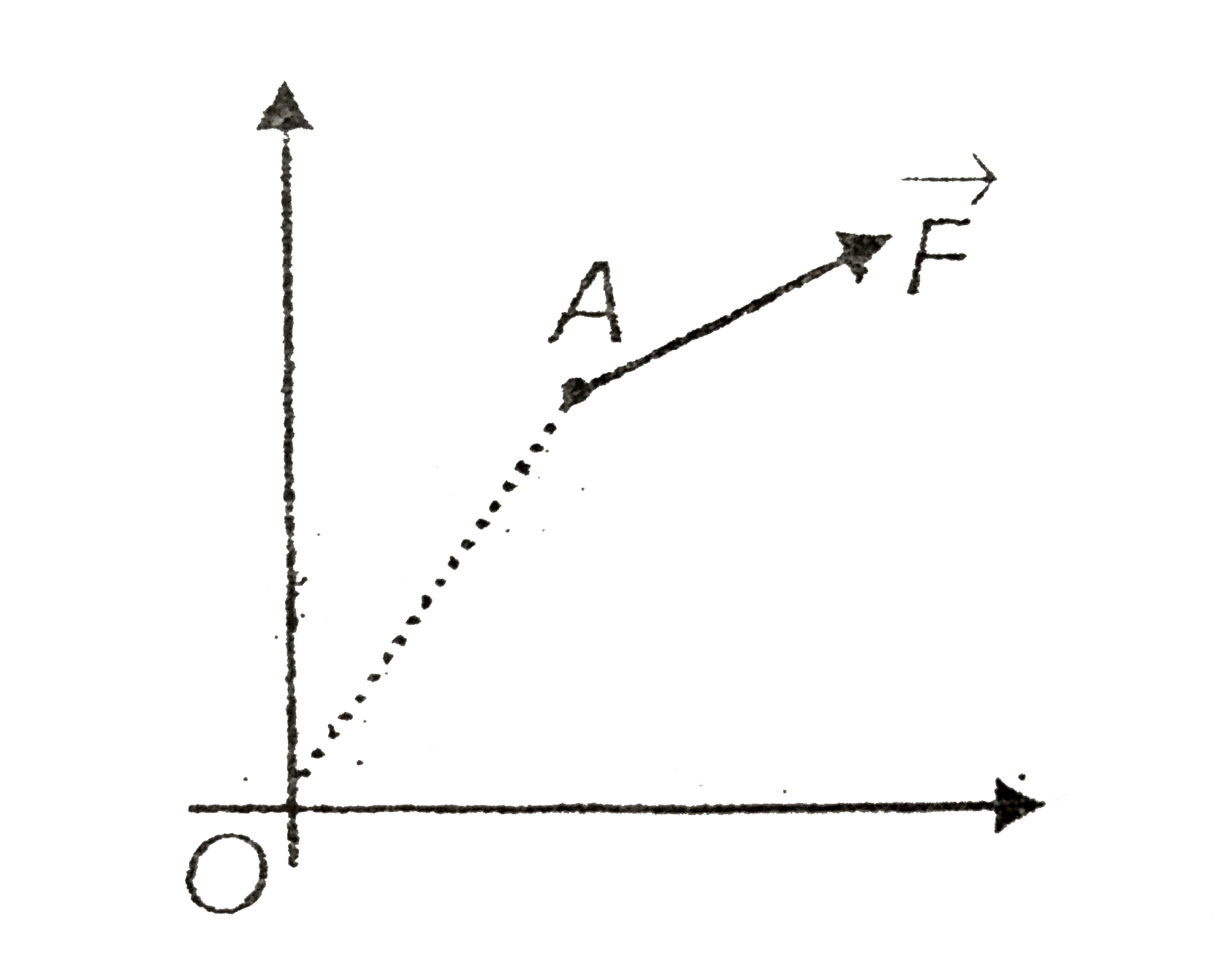
View SolutionA force →F=(3ˆi+4ˆj)N is acting on a point mass m=(12)kg at a point A(2m,2m). Find the angular acceleration of the line OA at this instant.
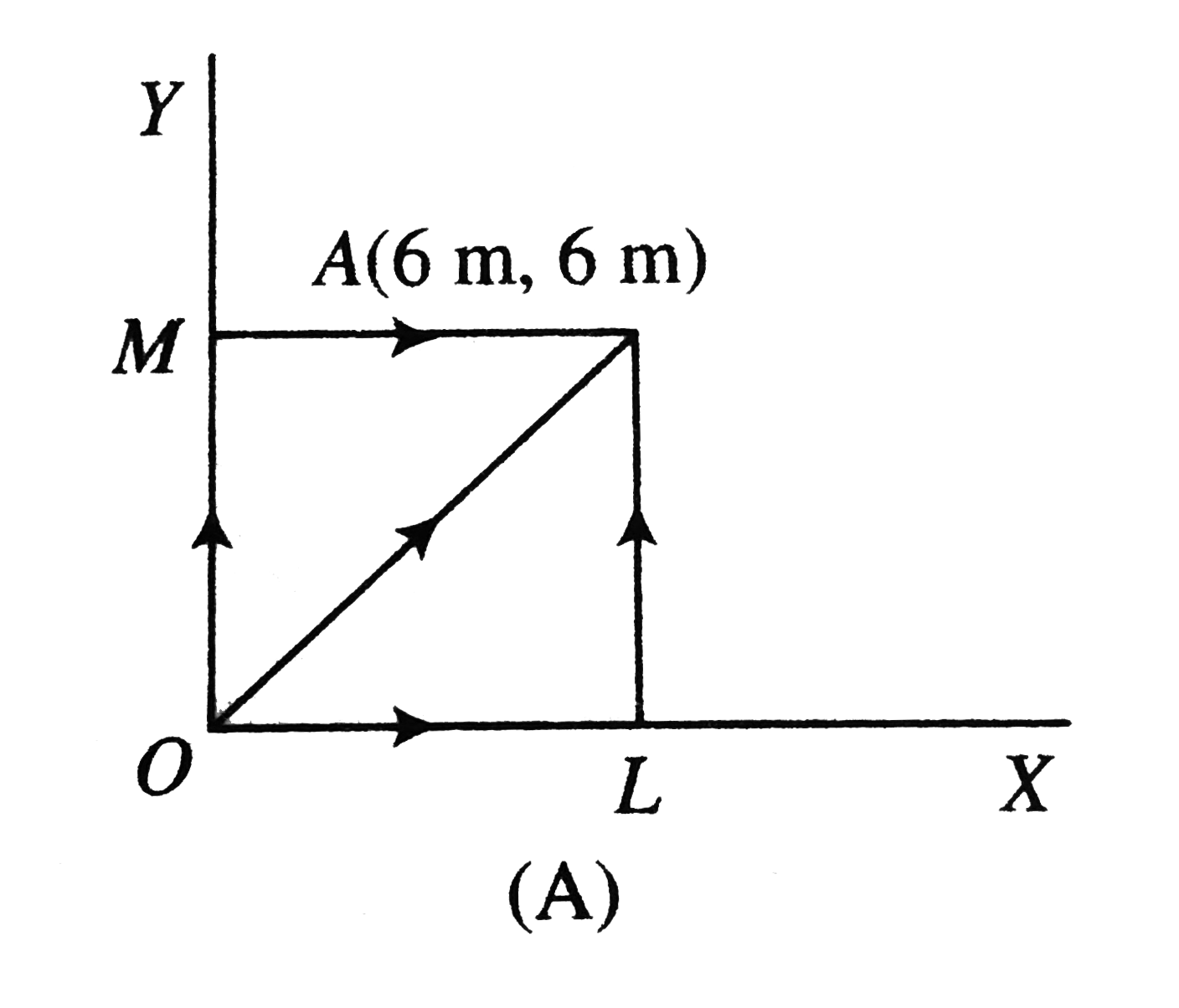
View SolutionForce acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
Now consider another situation. A force →F=(4ˆi+3ˆj)N acts on a particle of mass 2kg. The particle under the action of this force moves from the origin to a point A (4m,−8m). Initial speed of the particle, i.e., its speed at the origin is 2√6ms−1. Figure shows three paths for the motion of the particle from O to A.

Speed of the particle at A will be nearly
View SolutionForce acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
Now consider another situation. A force →F=(4ˆi+3ˆj)N acts on a particle of mass 2kg. The particle under the action of this force moves from the origin to a point A (4m,−8m). Initial speed of the particle, i.e., its speed at the origin is 2√6ms−1. Figure shows three paths for the motion of the particle from O to A.
If the potential energy at O is 16J, the potential energy at A will be
View Solution
