A ship is travelling due east at a speed of $15 k m / h .$ Find the speed of a boat heading $30^{\circ}$ east of north if it appears always due north from the ship.

A

30 km/h

B

$\frac{15 \sqrt{3}}{2} k \frac{m}{h}$

C

$10 \sqrt{3} k \frac{m}{h}$

D

$20 k \frac{m}{h}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

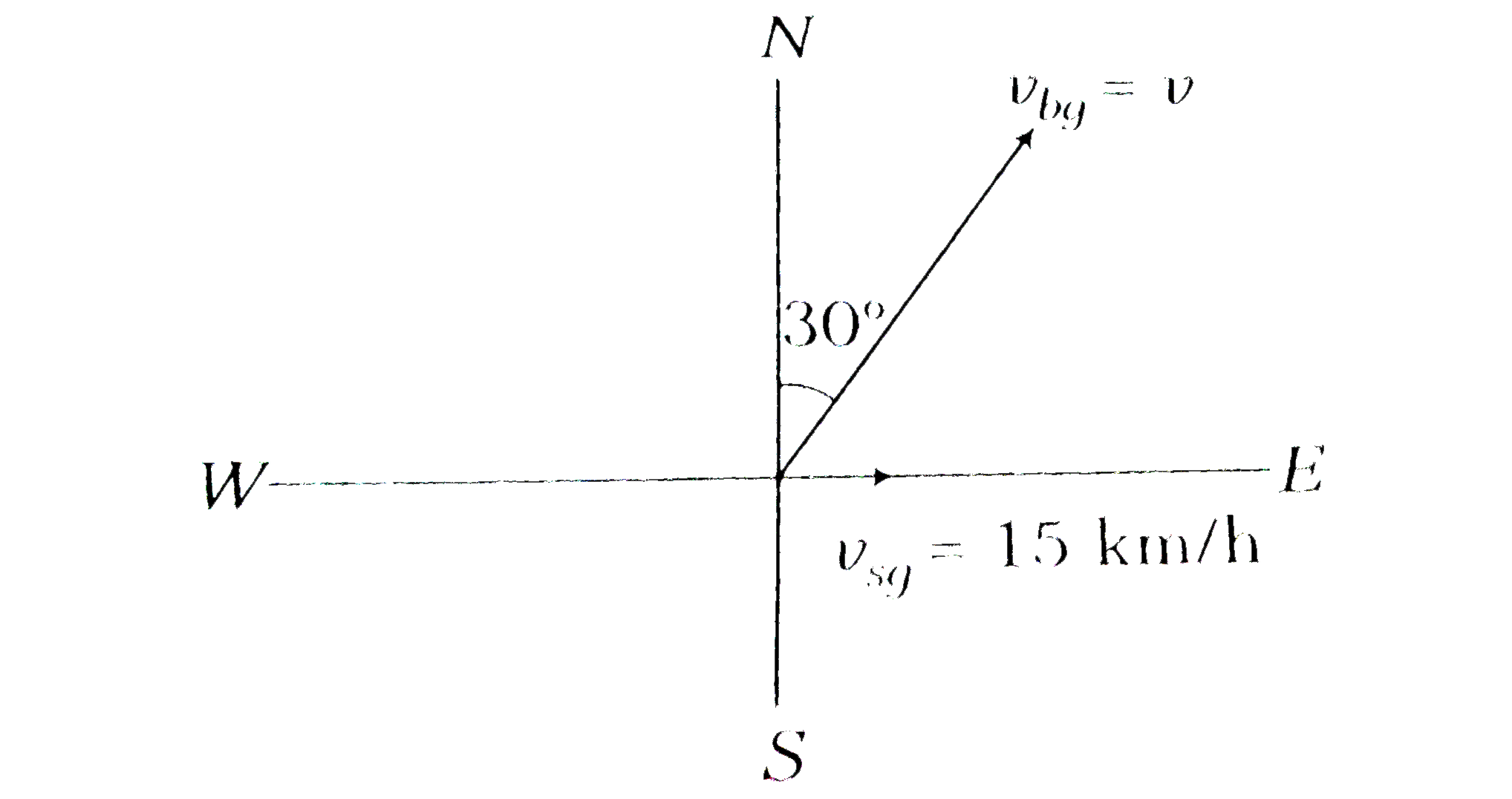
where $v_{b g}$ is the ship w.r.t. ground. Relative velocity of boat w.r.t. ship $υ_{b s}$ is along north. $υ_{b s}$ is resultant of $υ_{b g}$ and $υ_{b g}$ and $υ_{s g}$ in opposite direction.

$υ b {\cos 30}^{\circ} = υ_{b s}$
$υ {\sin 30}^{\circ} = 15 \Rightarrow υ 30 k m / h$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ship is travelling due east at 10 km/h. A ship heading $30^{\circ}$ east of north is always due north from the first ship. The speed of the second ship in km/h is
A $20 \sqrt{2}$
B $20 \sqrt{3 / 2}$
C $20$
D $20 / \sqrt{2}$
Question 2 - Select One
A ship is travelling due north at 40 kmph. The captain of the finds that a second ship is always sailing $60^{\circ}$ west of north at a speed of 40 kmph. The velocity of the second ship then must be
A40 kmph, $30^{\circ}$ west of north
B40 kmph. $60^{\circ}$ west of south
C $40 \sqrt{3}$ kmph, $30^{\circ}$ west of north
D $40 \sqrt{3}$ kmph, $60^{\circ}$ west of south
Question 3 - Select One
Ship $A$ is travelling with a velocity of $5 k m h^{- 1}$ due east. A second ship is heading $30^{\circ}$ east of north. What should be the speed of second ship if it is to remain always due north with respect to the first ship ?
A $10 k m h^{- 1}$
B $9 k m h^{- 1}$
C $8 k m h^{- 1}$
D $7 k m h^{- 1}$

DC PANDEY-MOTION IN A PLANE-(A) Taking it together

Home
Ask Doubt
Profile