Particle A is moving along X-axis. At time t = 0, it has velocity of 10ms−1 and acceleration −4ms−2. Particle B has velocity of 20ms−1 and acceleration −2ms−2. Initially both the particles are at origion. At time t = 2 distance between the particles are at origin. At time t = 2 s distance between the particles is
24 m
36 m
20 m
42 m
The correct Answer is:A
At t=2s:xA=10×2−12×4×(2)2=12m
and xB=20×2−12×2×(2)2=36m
∴ Distance between A and B at that instant is 24 m.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Assertion and reason)19videos
MOTION IN A PLANE
- BOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)6videos
MOTION IN A PLANE
- BOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.715videos
MOTION IN A PLANE
- BOOK - DC PANDEYCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
A particle is moving with initial velocity 1m/s and acceleration a=(4t+3)ms2. Find velocity of particle at t=2sec.
View SolutionThe acceleration of a particle is increasing linearly with time t as bt .The particle starts from the origin with an initial velocity v_(0) The distance travelled by the particle in time t will be
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle has initial velocity 4i+4jms−1 and an acceleration −0.4ims−2, at what time will its speed bbe 5ms−1?
A2.5 sB17.5 sCsD8.5 s - Question 2 - Select One
The acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
Av0t+16bt3Bv0t+13bt3Cv0t+13bt2Dv0t+12bt2 - Question 3 - Select One
The acceleration of particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be.
Av0t+13bt2Bv0t+13bt3Cv0t+16bt2Dv0t+12bt2
A particle moves in the x-y plane according to the law x=t2, y = 2t. Find:
(a) velocity and acceleration of the particle as a function of time,
(b) the speed and rate of change of speed of the particle as a function of time,
(c) the distance travelled by the particle as a function of time.
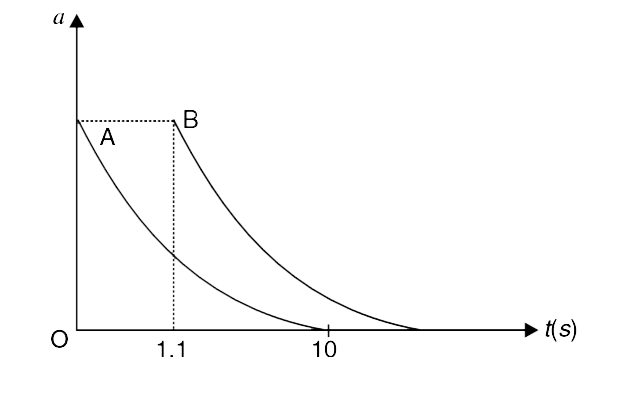
(d) the radius of curvature of the particle as a function of time.View SolutionParticle A starts from rest and moves along a straight line. Acceleration of the particle varies with time as shown in the graph. In 10 s the velocity of the particle becomes 60m/s and the acceleration drops to zero. Another particle B starts from the same location at time t=1.1s and has acceleration – time relationship identical to A with a delay of 1.1s. Find distance between the particles at time t=15s.
 View Solution
View SolutionA particle starts moving in +ve x direction with initial velocity of 10ms−1 with a uniform acceleration of magnitude 2ms−2 but directed in -ve x direction. What is the distance traversed by the particle in 12 seconds:
View SolutionA particle has an initial velocity of 5.5ms−1 due east and a constant acceleration of 1ms−2 due west. The distance covered by the particle in sixth second of its motion is.
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View Solution

