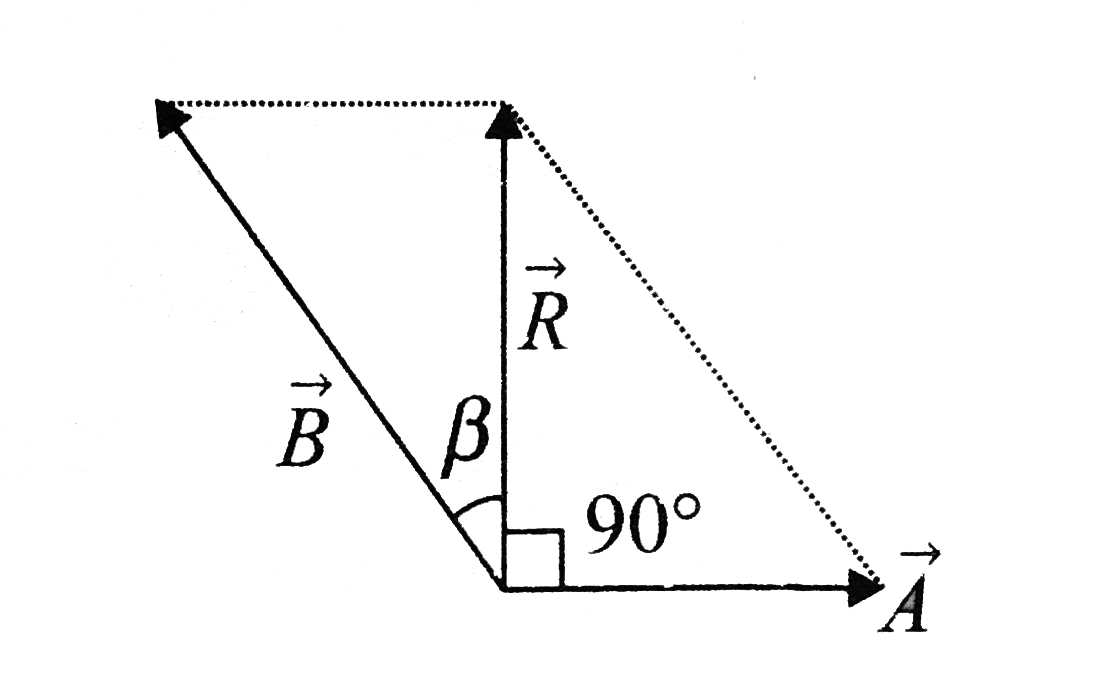
The resultant of →a and →b makes α with →a and β with →b, then (a,b represent magnitudes of respective vectors) :
apha<β
α>βifA<B
α<βifA=B
α<βifA<B
The correct Answer is:B
(b) Resultant is inclined towards a vector having greater magnitude
Topper's Solved these Questions
Similar Questions
The resultant of two velocity vectors →A and →B is perpendicular to →A. Magnitude of Resultant →R is equal to half magnitude of →B. If the angle between →A and →B is (30θ)∘, then value of θ is ?
View SolutionThe resultant of two vectors →Aand→B perpendicular to the vector →Aanditsmagnitudequal→halfofthemagnitudeofthe→−−→r vec B.F∈doutthe∠between vec A and vec B.
View Solution
Knowledge Check
The resultant of →A and →B makes an angle α with →A and ω with →B , then:-
Aα<βBα<β if A<BCα<β if A>BDα<βif A=BThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
 A120∘B150∘C135∘DNone of these
A120∘B150∘C135∘DNone of theseThe resultant of two vectors →Aand→B is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. What is the angle between →Aand→B ?
A30∘B45∘C150∘D120∘
The magnitude of the resultant of →A+→B and →A−→B is
View SolutionIf →a and →b are two vectors such that (→a+→b).→a−→b=0 find the relation between the magnitudes of →a and →b.
View Solutionthe resultant of two vectors →a&→b is perpendicular to →a. If ∣∣→b∣∣=√2|→a| show that the resultant of 2→a&→b is perpendicular to →b .
View SolutionTwo vectors →Aand→B inclined at an angle θ have a resultant →R which makes an angle α with →A. If the directions of →Aand→B are interchanged, the resultant will have the same
View SolutionIf →a.→b=∣∣→a×→b∣∣, then angle between vector →a and vector →b is :
View Solution
