An Lc circuit contains a 40 mH inductor and a 25μF capacitor. The resistance of the circuit is negligible.The time is measured from the instant the circuit is closed. The energy stored in the circuit is completely magnetic at time (in milliseconds)
0,3.14,6.28
0,1.57,4.71
1.57,4.71,7.85
1.57,3.14,4.71
The correct Answer is:C
Here, L=40mH=40×10−3H
C=25μF=25×10−6F,υ=12π√LC
Substituting the given values, we get
υ=12π√40×10−3×25×10−6=1032πHz
∴T=1υ=2π103s=2π×10−3s=2πms
Energy stored is completely electrical at times
t=0,T2,T,32T, .......
Energy stored is completely magnetic at times
t=T4,34T,54T, .........
Hence, t=π2ms,3π2ms,5π2ms=1.57ms,4.71ms,7.85ms
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - NCERT FINGERTIPSCHAPTER - ALTERNATING CURRENT EXERCISE - Transformers
16 Videos
- ALTERNATING CURRENT BOOK - NCERT FINGERTIPSCHAPTER - ALTERNATING CURRENT EXERCISE - Higher Order Thinking Skills
8 Videos
- ALTERNATING CURRENT BOOK - NCERT FINGERTIPSCHAPTER - ALTERNATING CURRENT EXERCISE - Power In Ac Circuit
13 Videos
- ATOMS BOOK - NCERT FINGERTIPSCHAPTER - ATOMS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
What is the energy stored in a pure LC circuit ?
View SolutionAn L-C circuit contains 20 mH inductor and a 50μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant the circuit is closed be t = 0. what is the total energy stored initially ? At what times is the total energy shared equally between the inductor and the capacitor ?
View Solution
Knowledge Check
An LC circuit contains a 20mH inductor asn a 50μF capacitor with initial change of 10mC. The resistance of the circuit is negligible. Let the instant the circuit is closed be t=0.
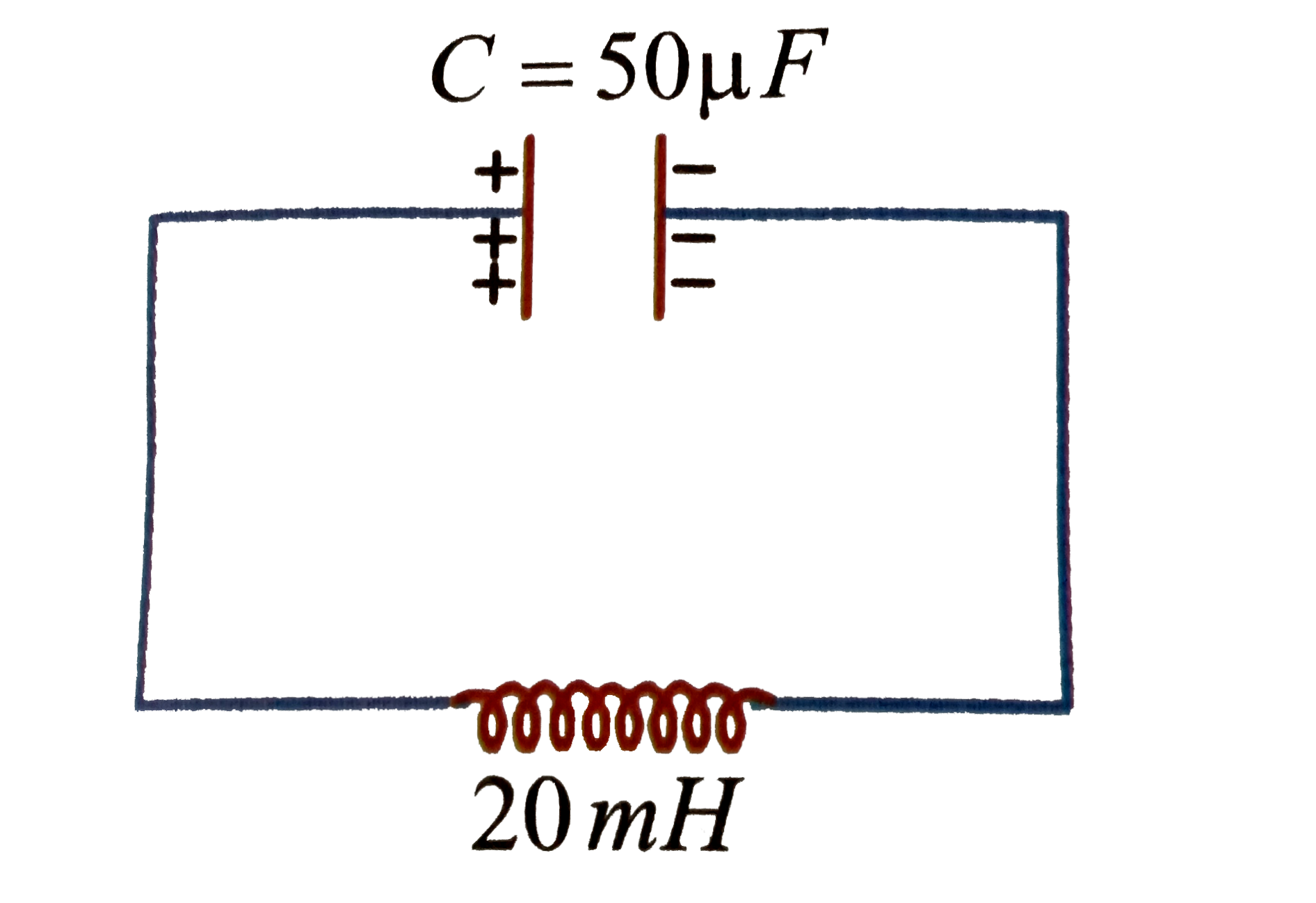 AEnergy stored in the circuit in completely electrical at t=nπ2000BEnergy stored in the circuitin completely magnetic at t=(2n+1)π2000CEnergy stored in the circuit in shared equally between the inductor and capacitor at t=(2n+1)π4000DEnergy stored in the circuit is shared euqally between the inductor and capacitor at t=nπ2000
AEnergy stored in the circuit in completely electrical at t=nπ2000BEnergy stored in the circuitin completely magnetic at t=(2n+1)π2000CEnergy stored in the circuit in shared equally between the inductor and capacitor at t=(2n+1)π4000DEnergy stored in the circuit is shared euqally between the inductor and capacitor at t=nπ2000An LC circuit contains a 20 mH inductor and a 50μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant at which the circuit which is closed be t=0. At what time the energy stored is completely magnetic ?
At = 0Bt=1.54msCt=3.14msDt=6.28msIn the circuit shown, the energy stored in 1μF capacitor is
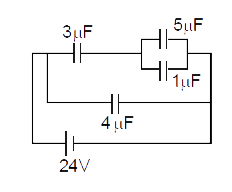 A40μJB64μJC32μJDnone of these
A40μJB64μJC32μJDnone of these
An LC circuit contains a 20 mH inductor and a 50 uF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant, the circuit is closed be t = 0.
(a) What is the total energy stored initially ? Is it conserved during LC oscillations ?
(b) What is the natural frequency of the circuit ?
(c) At what time is the energy stored
(i) completely electrical (i.e., stored in the capacitor)?
(ii) completely magnetic (i.e., stored in the inductor)?
(d) At what times is the total energy shared equally between the inductor and the capacitor ?
(e) If a resistor is inserted in the circuit, how much energy is eventually dissipated as heat ?
View SolutionAn LC circuit contains a 20 mH inductor and a 50μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant the circuit is closed be t = 0.
(a) What is the total energy stored initially ? Is it conserved during the oscillalions?
(b) What is the natural frequency of the circuit?
(c ) At what time is the energy stored? (i) Completely electrical ? (ii) Completely magnetic ?
(d) At what time is the total energy shared equally between the inductor and the capacitor ?
(e) If a resistor is inserted in the circuit, how much energy is eventually dissipated as heat ?
View SolutionIn an LC circuit, resistance of the circuit is negligible. If time period of oscillation is T then :
(ii) at what time is the energy stored completely magnetic
View SolutionIn the circuit shown, the energy stored in 1μF capacitor is
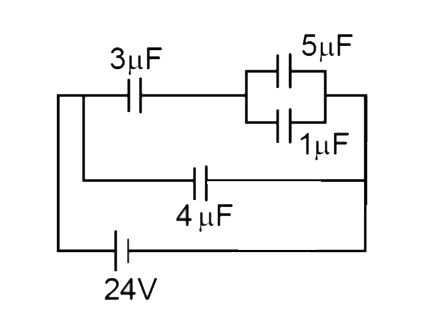
View SolutionAn l-C circuit contains 10 mH inductor and a 25 μF capacitor. The ratio of the time periods for the energy to be completely magnetic, is
View Solution
