A stone of mass $m$ is tied to one end of a wire of length $L$ . The diameter of the wire is $D$ and it is suspended vertically. The stone is now rotated in a horizontal plane and makes an angle $θ$ with the vertical. If Young's modulus of the wire is $Y$ , then the increase in the length of the wire is

A

$\frac{4 m g l}{π D^{2} Y}$

B

$\frac{4 m g l}{π D^{2} Y sin θ}$

C

$\frac{4 m g l}{π D^{2} Y cos θ}$

D

$\frac{4 m g l}{π D^{2} Y tan θ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

The situation is as shown in the figure. For vertical equilibrium of stone

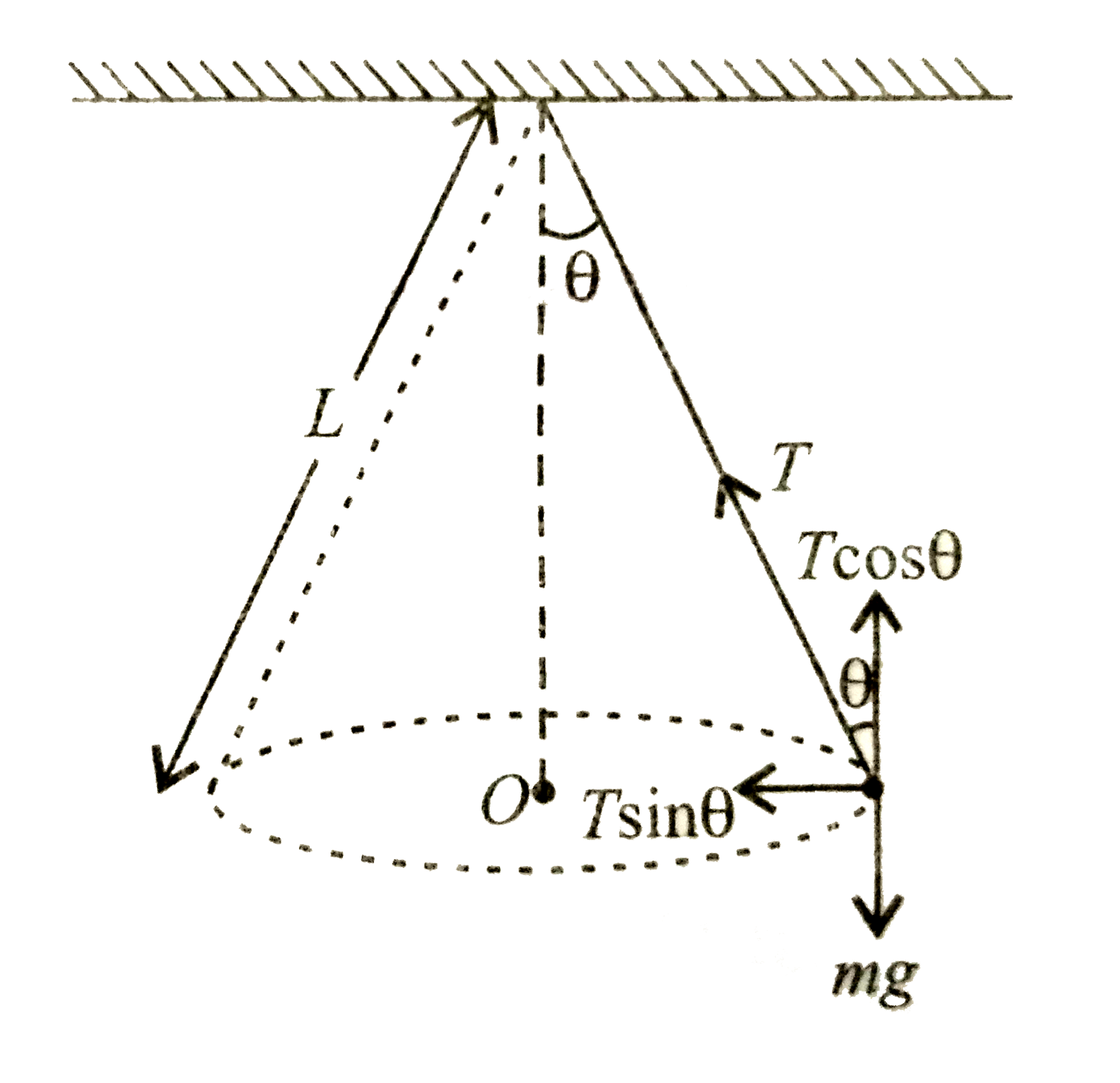
$T cos θ = m g or T = \frac{m g}{cos θ} ... . . (i)$
As $Y = \frac{T}{A} \frac{L}{Δ L}$
$∴ Δ L = \frac{T L}{A Y} (Using (i))$
$= \frac{m g L}{cos θ (π D^{2} / 4) Y} = \frac{4 m g l}{π D^{2} Y cos θ}$

|

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A stone of mass $m$ tied to one end of a wire of length L. the diameter of the wire is D and it is suspended vertically. The stone is now rotated in a horizontal plane and makes an angle 6 with the vertical. If Young's modulus of the wire is $Y$ , Then the increase in the length of the wire is
A $\frac{4 m g L}{π D^{2} Y}$
B $\frac{4 m g L}{π D^{2} Y sin θ}$
C $\frac{4 m g L}{π D^{2} Y cos θ}$
D $\frac{4 m g L}{π D^{2} Y tan θ}$
Question 2 - Select One
An iron wire of length 4 m and diameter 2 mm is loaded with a weight of 8 kg. if the Young's modulus Y for iron is $2 \times 10^{11} N / m^{2}$ then the increase in the length of the wire is
A0.2 mm
B0.5 mm
C2 mm
D1 mm
Question 3 - Select One or More
A uniform wire of radius r and length L hanging vertically and fixed at its upper ends, is attached to a weight at its lower end. If Young's modulus for the material of the wire is Y, the extension is
Ainversely proportional to Y.
Binversely proportional to $r^{2}$ .
Cdirectly proportional to L.
Dinversely proportional to r.

NCERT FINGERTIPS-MECHANICAL PROPERTIES OF SOLIDS-Elastic Moduli

Home
Ask Doubt
Profile