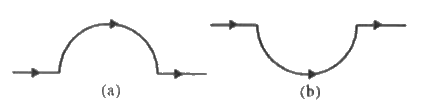
चित्र में दर्शाए अनुसार किसी सीधे तार जिसमें 12 A विद्युत धारा प्रवाहित हो रही है को 2.0 cm त्रिज्या के अर्धवृत्ताकार चाप में मोड़ा गया है। इस चाप के केंद्र पर चुंबकीय क्षेत्र →B को मानें।
a. सीधे खंडों के कारण चुम्बकीय क्षेत्र कितना है?
b. किस रूप में अर्धवृत्त द्वारा →B को दिया गया योगदान वृत्ताकार पाश के योगदान से भिन्न है और किस रूप में ये एक दूसरे के समान है?
c. क्या आपके उत्तर में कोई परिवर्तन होगा यदि तार को उसी त्रिज्या के अर्द्धवृत्त में पहले की तुलना में चित्र b में दर्शाए अनुसार उल्टी दिशा में मोड़ दें?
चित्र में दर्शाए अनुसार किसी सीधे तार जिसमें 12 A विद्युत धारा प्रवाहित हो रही है को 2.0 cm त्रिज्या के अर्धवृत्ताकार चाप में मोड़ा गया है। इस चाप के केंद्र पर चुंबकीय क्षेत्र vecB को मानें। a. सीधे खंडों के कारण चुम्बकीय क्षेत्र कितना है? b. किस रूप में अर्धवृत्त द्वारा vecB को दिया गया योगदान वृत्ताकार पाश के योगदान से भिन्न है और किस रूप में ये एक दूसरे के समान है? c. क्या आपके उत्तर में कोई परिवर्तन होगा यदि तार को उसी त्रिज्या के अर्द्धवृत्त में पहले की तुलना में चित्र b में दर्शाए अनुसार उल्टी दिशा में मोड़ दें?

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

a.सीधे खण्डों के लिए d→l∣∣→r अतः →dl×→r=0 अतः चाप के केंद्र पर सीधे खण्डों द्वारा चुम्बकीय क्षेत्र में कोई योगदान नहीं है।
b. किसी वृत्ताकार पाश के कारण केंद्र पर चुम्बकीय क्षेत्र की तीव्रता ∣∣→B∣∣=μ0I2R होता है जबकि अर्द्धवृत्ताकार पाश के कारण चुम्बकीय क्षेत्र की तीव्रता ∣∣→B∣∣=μ0I4R होता है अतः दिए गए प्रश्नानुसार अर्द्धवृत्ताकार पाश द्वारा उत्पन्न चुम्बकीय क्षेत्र ∣∣→B∣∣=4π×10−7×124×2×10−20=1.884×10−4 टेसला।
इसकी दिशा दक्षिणाहस्त पेंच नियम से कागज के तल में लम्बवत अंदर की ओर होगी।
c. इस स्थिति में चाप के केंद्र पर चुम्बकीय क्षेत्र का परिमाण वही रहेगा केवल दिशा विपरीत कागज के तल के लम्बवत बाहर की ओर होगी।

Updated on:21/07/2023
|
Class 12PHYSICSMOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions