The linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
Let us consider a small length dx of the rod shown in the figure.
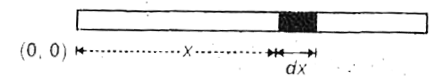
Its mass dm=λdx=(1+2x)dx
Xcm=∫xdm∫dm=∫10x(1+2x)dx∫10(1+2x)dx=[x22+2x33]10[x+x2]10=712m
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE
9 Videos
Similar Questions
Knowledge Check
If the linear density (mass per unit length) of a rod of length 3m is proportional to x, where x, where x is the distance from one end of the rod, the distance of the centre of gravity of the rod from this end is.
A2.5 mB1 mC1.5 mD2 mThe mass per unit length of a non - uniform rod of length L is given μ=λx2 , where λ is a constant and x is distance from one end of the rod. The distance of the center of mas of rod from this end is
AL2BL4C3L4DL3The mass per unit length of a non-uniform rod of length L is given by μ=λ×2, where λ is a constant and x is distance from one end of the rod. The distance of the center of mass of rod from this end is :-
AL2BL4C3L4DL3
The linear mass density of a thin rod AB of length L varies from A to B as λ(x)=λ0(1+xL). Where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicualr to the rod is :
View SolutionThe density of a thin rod of length l varies with the distance x from one end as ρ=ρ0x2l2. Find the position of centre of mass of rod.
View SolutionThe mass per unit length of a non- uniform rod OP of length L varies as m=k(x)/(L) where k is a constant and x is the distance of any point on the rod from end 0 .The distance of the centre of mass of the rod from end 0 is
View SolutionA heavy metallic rod of non-uniform mass distribution, is hanged vertically from a rigid support. The linear mass density varies as λ(x)=k×x where x is the distance measured along the length of rod, from its lower end. Find extension in rod due to its own weight.
View SolutionFind centre of mass of given rod of linear mass density λ=(a+b(xl)2) , x is distance from one of its end. Length of the rod is l.
View Solution

