The displacement s of an object is given as a function of time t by the following equation s=2t+5t2+3t3. Calculate the instantaneous velocity of the object at t = 1 s.
The correct Answer is:21m/s
v=dsdt
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE
30 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - A)
60 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
4 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
A particle moves along a circular path of radius R. The distance and displacement of the particle after one complete revolution is
View SolutionA body in one dimensional motion has zero speed at an instant. At that instant, it must have
View SolutionA : It is not possible to have constant velocity and variable acceleration.
R : Accelerated body cannot have constant velocity.
View SolutionThe maximum angle to the horizontal at which a stone can be thrown so that it always moves away from the thrower will be :
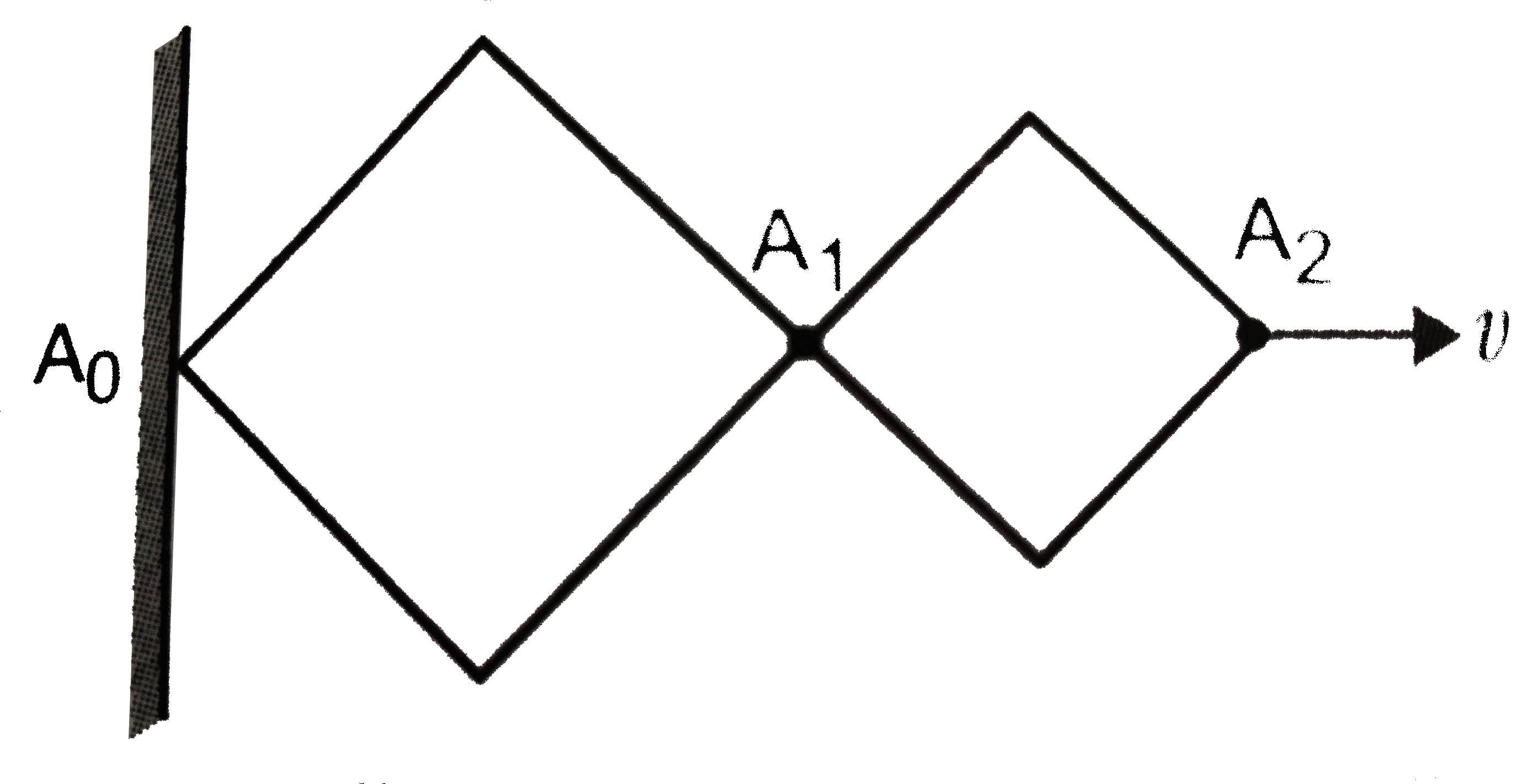
View SolutionThe given construction as shown in Fig. 2 (HT) .3, consists of two rhombus with the ratio 3:2, The vertex A2 moves In the horizontal direction with a velocity v. Find the velocity of A1.
View SolutionThe displacement x of an object is given as a funstion of time, x=2t+3t2. The instantaneous velocity of the object at t = 2 s is
View SolutionThe displacement x of an object is given as a function of time x=2t+3t2
Calculate the instantaneous velocity of the object at t = 2 s
View SolutionThe velocity of an object is changing with time and relation is given by the following equation.
v=2t+3t2
Calculate the position of the object from the origin at t = 2 s.
Assume particle to be at origin at t = 0
View SolutionThe displacement s of an object is given as a function of time t
s=5t2+9t
Calculate the instantaneous velocity of object at t = 0.
View SolutionThe displacement s of an object is given as a function of time t by the following equation s=2t+5t2+3t3. Calculate the instantaneous velocity of the object at t = 1 s.
View SolutionIf displacement S at time t is S=−t3+3t2+5, then velocity at time t=2 sec is
View Solutionविस्थापन S व समय t सूत्र S=2t2+5t+9 से सम्बन्ध है। समय t=2 सेकण्ड पर त्वरण होता है-
View Solution[" A particle is moving along "],[" a straight line with non- "],[" uniform acceleration.The "],[" displacement of the "],[" particle is given by "],[S=2t^(3)+3t^(2)+5t" where "S" is in "],[" metres and "t" is in seconds."],[" The velocity of the particle "],[" at "t=2" seconds is "]
View Solution[" A particle is moving along "],[" a straight line with non- "],[" uniform acceleration.The "],[" displacement of the "],[" particle is given by "],[S=2t^(3)+3t^(2)+5t" where "S" is in "],[" metres and "t" is in seconds."],[" The velocity of the particle "],[" at "t=2" seconds is "]
View SolutionThe velocity of an object is changing with time and relation is given by the following equation. v=2t+3t^(2) Calculate the position of the object from the origin at t=2s.
View SolutionThe velocity of an object moving in a straight line path is given as a function of time by v=6t-3t^2 , where v is in ms^-1 , t is in s. The average velocity of the object between , t=0 and t=2 s is
View Solution
