Question

Volume of pyramid

Explanation

Volume of Pyramid

In this chapter, we will study volume of pyramid. We will also learn the formula for volume of pyramid as well as the pyramid triangle.  You would also be able to work on some examples where it would lead to getting the right and clear idea of it. It is important to note that the volume of pyramid is dependent on the type of the base of the pyramid. So, it depends on whether the base is a square, triangle or rectangle. It proves to be a poly sided figure when it comes to the base of the pyramid. So, it is on the basis of the structure  of the height and the base of the pyramid that is required for the formula to find out its volume and also its surface area. Let us go ahead and learn more about it in the best way. 

The derivation of Volume of a Pyramid

It is quite important to get the right knowledge of the total capacity of the given pyramid when you need to find the volume of a pyramid. Coming to the formula for the volume of a pyramid, it is given as :

Volume = 1/3 x Area of the Base x Height or

V = (1/3) A x H

Here, A = Area, H = height and V = Volume

It is the following units that the volume of a pyramid is measured

It’s volume is measured in the  following units:

• ft³


• in³


• cm³


• m³ etc

While calculating the volume, it is always important to keep all the measurement units the same. We will study the formula for the different types of pyramids.

Formula for Volume of Pyramid

 

Volume of Triangular Pyramid

There is a triangular base in this type of pyramid. We know that the area of a triangle is

A= ½ b x h, be is the base and ‘h’ is the height of triangle.

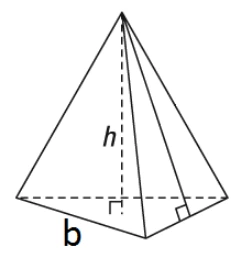
So, when it comes to the volume of a triangular pyramid;

V = 1/3 x Area of base x Height of pyramid

V = 1/3 x (1/2 b.h) x H

V = 1/6 bhH

Volume of Rectangular Pyramid

There is a presence of a base in the shape of a rectangle in a rectangular pyramid. The product of its length and width is the area of the rectangle where,

A = Length x Width

A = lw

 

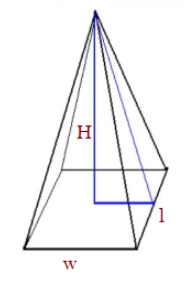
So, when it comes to the volume of a rectangular pyramid, it is given by:

V = 1/3 x A x H

V = 1/3 lwH

Volume of Square Pyramid

When it comes to the square-based pyramid, it has a square base. We are familiar that the area of a square is given by;

A = a², Here, the length of the side of the square is ‘a’.

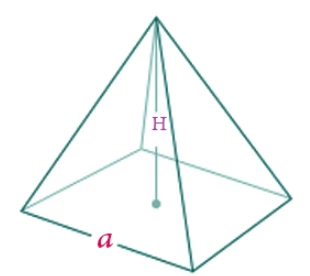
So, coming to the volume of a square-sided pyramid, it is;

V = 1/3 x Area of square base x Height

V = 1/3 x a² x H

V = 1/3 a² H

Volume of Hexagonal Pyramid

When it comes to the volume of a hexagonal pyramid, it has got the base in a regular hexagon shape which is given by:

Volume = 1/3 x area of base x height

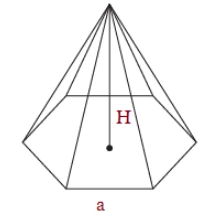
V= 1/3 x 3√3/2 a² x H

V = √3/2 a² H

Here ‘a’ is the side length of the hexagon base, whereas H is the height of the pyramid.

Related Videos:

• Surface area of pyramid


• Volume of a cube


• Volume of a cuboid


• Volume and surface area of cone


• Volume of Sphere and Hemisphere

We will now concentrate on some examples to get a clear idea on how to solve different questions:

Problem 1: The base of a pyramid is square in shape. When it comes to the sides of the base, they are 10 cm each where the height of the pyramid is 21cm. Can you find out the volume of the pyramid?

Solution: To find the volume of a pyramid, we will use the formula – V = ⅓ A H

According to the question, the base of the pyramid is a square. Here, will find the area of the base, which is:

a² = 10 x 10 = 100 cm²

= ⅓ x 100 cm ² x 21 cm

= 100 x 7

= 700 cm³

Therefore the volume of the pyramid is 700 cm³.

Problem 2: The base of a pyramid is square in shape. The sides of the base are 14 cm each, and the height is 21cm. Can you find the volume of the pyramid?

Solution: When it comes to finding the volume of a pyramid, we make use of the formula – V = ⅓ A H

It is given that the base of the pyramid is a square. Here, the area of the base is

a² = 14 x 14 = 196cm²

= ⅓ x 196 cm ² x 21 cm

= 196 x 7

= 1102 cm³

Therefore the volume of the pyramid is 1102 cm³.

Problem 3: The base of the pyramid is rectangular in shape. It has got a length of 9   cm, and the width is 7 cm, and the height of the pyramid is 10cm. Can you find its volume?

Solution: Given, the length of rectangular base of pyramid = 9 cm

width = 7 cm

and height of the pyramid = 10cm

We know, the volume of rectangular pyramid,

V = 1/3 l w H

Substituting the values we get;

V = 1/3 x 9 x 7 x 10

V = 630/3 = 210 cm³

Therefore the volume of the pyramid is 210 cm³.

Problem 4: The area of the base of a triangular pyramid is 165 cubic cm. The height is 7 cm. Can you find its volume?

Solution: Given the area of the base of pyramid = 165 cu.cm

We know that

Volume of pyramid = 1/3 x A x H

So, V = 1/3 x 165 x 7

      V = 55 x 7

      V = 385 cm³.

Important Chapters:

• NCERT Solutions for Maths


• NCERT Solution for Class 6 Maths Chapter Mensuration


• NCERT Solution for Class 8 Maths Chapter Mensuration


• NCERT Solution for Class 8 Maths Chapter Visualising Solid Shapes