Four equal electric charges are arranged at the four corners of a square of side 'a'. Out of these four charges, two charges are positive and placed at the ends of one diagonal. The other two charges are positive and placed at the ends of the other diagonal. The energy of the system in
negative
positive
less than 14πε0(2q2a)
greater than 14πε0(2q2a)
The correct Answer is:B, D
To find the total energy of the system of four equal positive charges arranged at the corners of a square, we can follow these steps:
Step 1: Understand the Configuration
We have four equal positive charges Q placed at the corners of a square with side length a. The charges are arranged such that two charges are at the ends of one diagonal and the other two charges are at the ends of the other diagonal.
Step 2: Identify the Pairs of Charges
We need to calculate the potential energy for each unique pair of charges. The pairs are:
1. Charges at corners A and B
2. Charges at corners B and C
3. Charges at corners C and D
4. Charges at corners D and A
5. Charges at corners A and C (diagonal)
6. Charges at corners B and D (diagonal)
Step 3: Calculate the Potential Energy for Each Pair
The potential energy U between two point charges Q1 and Q2 separated by a distance r is given by:
U=kQ1Q2r
where k=14πϵ0.
For adjacent charges (A-B, B-C, C-D, D-A):
- The distance r=a.
- The potential energy for each pair is:
UAB=UBC=UCD=UDA=kQ2a
For diagonal charges (A-C, B-D):
- The distance r=√2a.
- The potential energy for each diagonal pair is:
UAC=UBD=kQ2√2a
Step 4: Total Potential Energy of the System
Now we can sum the potential energies of all pairs:
Utotal=UAB+UBC+UCD+UDA+UAC+UBD
Substituting the values:
Utotal=4(kQ2a)+2(kQ2√2a)
Step 5: Simplifying the Expression
Factor out kQ2/a:
Utotal=kQ2a(4+21√2)
Calculating 2/√2=√2:
Utotal=kQ2a(4+√2)
Step 6: Final Expression
Thus, the total energy of the system is:
Utotal=kQ2a(4+√2)
Step 7: Conclusion
Since k and Q2/a are both positive constants, the total energy Utotal is positive.
We have four equal positive charges Q placed at the corners of a square with side length a. The charges are arranged such that two charges are at the ends of one diagonal and the other two charges are at the ends of the other diagonal.
We need to calculate the potential energy for each unique pair of charges. The pairs are:
1. Charges at corners A and B
2. Charges at corners B and C
3. Charges at corners C and D
4. Charges at corners D and A
5. Charges at corners A and C (diagonal)
6. Charges at corners B and D (diagonal)
The potential energy U between two point charges Q1 and Q2 separated by a distance r is given by:
U=kQ1Q2r
where k=14πϵ0.
- The distance r=a.
- The potential energy for each pair is:
UAB=UBC=UCD=UDA=kQ2a
- The distance r=√2a.
- The potential energy for each diagonal pair is:
UAC=UBD=kQ2√2a
Now we can sum the potential energies of all pairs:
Utotal=UAB+UBC+UCD+UDA+UAC+UBD
Substituting the values:
Utotal=4(kQ2a)+2(kQ2√2a)
Factor out kQ2/a:
Utotal=kQ2a(4+21√2)
Calculating 2/√2=√2:
Utotal=kQ2a(4+√2)
Thus, the total energy of the system is:
Utotal=kQ2a(4+√2)
Since k and Q2/a are both positive constants, the total energy Utotal is positive.
Topper's Solved these Questions
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - COMPREHENSION BASED (COMPREHENSION - II)
3 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - (PROBLEM SOLUTION) COMPREHENSION - I (COMPREHENSION BASED TYPE)
3 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL - I
24 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBOOK - FIITJEECHAPTER - ELECTROMAGNETIC WAVE & WAVE OPTICSEXERCISE - ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
21 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
Similar Questions
Knowledge Check
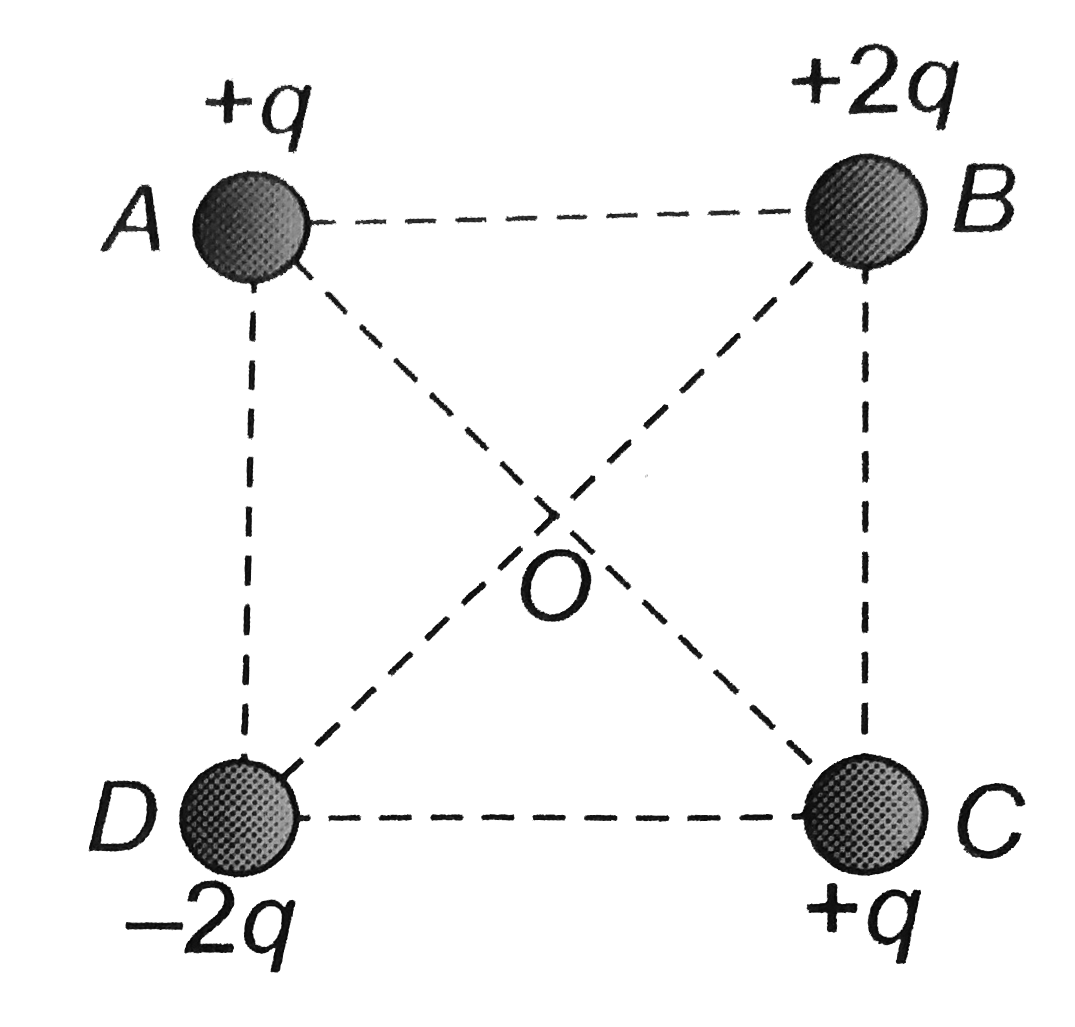
Four charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the centre O will be:
 AzeroBalong the diagonal ACCalong the diagonal BDDperpendicular to side AB
AzeroBalong the diagonal ACCalong the diagonal BDDperpendicular to side ABEqual charges q are placed at the four corners A,B,C,Dof a square of length a. The magnitude of the force on the charge at B will be
A3q24πε0a2B4q24πε0a2C(1+2√22)q24πε0a2D(2+1√2)q24πε0a2Four equal charges Q are placed at the four corners of a square of each side is 'a'. Work done in removing a charge −Q from its centre to infinity is
A0B√2Q24πε0aC√2Q2πε0aDQ22πε0a
Four equal point harges each 16μC are placed on the four corners of a square of side 0.2 m. Calculate the force on any one of the charges.
View SolutionFour charges are arranged at the corners of a square ABCD, as shown in the adjoining figure, The force on a positive charge kept at the centre O is
View SolutionEqual charges Q are placed at the four corners A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be
View SolutionFour charges are arranged at the corners of a square ABCD, as shown. The force on a positive charge kept at the centre of the square is

View SolutionFour equal charges Q are placed at the four corners of a square of each side is 'a'. Work done in removing a charge −Q from its centre to infinity is
View Solution

 .
.