Prove that the area of the parallelogram formed by the lines xcosα+ysinα=p,xcosα+ys∈α=q,xcosβ+ysinβ=randxcosβ+ysinβ=sis±(p−q)(r−s)cosec(α−β).
pq+rs
|pqtanα+rstanβ|
|(p−q)(r−s)cosec(α−β)|
|(p−q)(r−s)tan(α+β)|
The correct Answer is:C
Step by step video, text & image solution for Prove that the area of the parallelogram formed by the lines xcosalpha+ysinalpha=p ,xcosalpha+ys inalpha=q ,xcosbeta+ysinbeta=ra n dx cosbeta+ysinbeta=si s+-(p-q)(r-s)cos e c(alpha-beta)dot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - II
20 Videos
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - COMPREHENSIONS
9 Videos
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - II
14 Videos
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Comprehension Type
6 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
328 Videos
Similar Questions
Prove that the area of the parallelogram formed by the lines xcosα+ysinα=p,xcosα+ys∈α=q,xcosβ+ysinβ=randxcosβ+ysinβ=sis±(p−q)(r−s)cosec(α−β).
View SolutionArea of the parallelogram whose sides are xcosα+ysinα=p,<br>xcosα+ysinα=q,<br>xcosβ+ysinβ=r,<br>xcosβ+ysinβ=s is ………..
View SolutionThe area of the parallelogram formed by the lines xcosα+ysinα=p,xcosα+ysinα=q,xcosβ+ysinβ=r and xcosβ+ysinβ=s for given values of p, q, r and s is least, if (α−β)= (A) ±π2 (B) π4 (C) π6 (D) π3
View SolutionIf pandp be the perpendicular form the origin upon the straight lines xsecθ+ycosecθ=aandxcosθ−ysinθ=acos2θ
Prove that : 4p2+p2=a2
View SolutionThe roots of The roots of both the equation sin2x+psinx+q=0andcos2x+rcosx+s=0 are αandβ, Then the value of sin(α+β)=
View SolutionThe perpendicular form the origin on the line joining the points P(rcosα,rsinα) and Q(rcosβ,rsinβ) divides PQ in the ratio 1 : k then principal value of cos−1(1k)
View SolutionIf the straight line xcosα+ysinα=p touches the curve x2a2+y2b2=1 , then prove that a2 cos2α+b2 sin2α=p2 .
View SolutionThree points A,B,C are in a line inclined at an angle θ to the horizon of three points. A is the lowest and C is highest. D is a point vertically above C. if AB=p,CD=q,∠DAB=αand∠DBC=β, then
cosθ=psinαcosβqsin(β−α)
View SolutionP(α,f(α)) and Q(β,f(β)) are ends of an arc in the first quadrant. The area bounded by the arc, ordinates through P and Q, and the x-axis is (A) ∫f(β)f(α)f−1(y)dy (B) ∫βαf−1(y)dy (C) ∫βαf(x)dx (D) ∫f(β)f(α)f(x)dx
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ
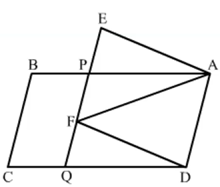
View Solution
