For a real number r we denote by [r] the largest integer less than or equal to r. If x,y are real numbers with x,y≥1 then which of the following statements is always true? A) [x+y]≤[x]+[y] B) [xy]≤[x][y] C) [2x]≤2x D)[xy]≤xy
[x+y]≤[x]+[y]
[xy]≤[x]+[y]
[2x]≤2[x]
[xy]≤[x][y]
The correct Answer is:D
(A) [x+y]≤[x]+[y]
let x=0.1
y=0.9
[0.1+0.9]≤[0.1]+[0.9]
1≤9+0 wrong
(B) [xy]≤[x]+[y]
x=2,y=12
[2⋅12]≤[2][12]
⇒1≤0 wrong
(C) [2x]≤2[x]
x=0.99[20.99]≤2[0.99]
[20.99]≤2∘=1 wrong
(D) [xy]≤[x][y]
given x,y≥1
if x<y[xy]=0 0≤[x][y] true
if x≥y[xy]≤[x][y] always true
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-II MATHEMATICS
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part A - Mathematics
20 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2(MATHEMATICS)
10 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
For a real number r we denote by [r] the largest integer less than or equal to r. If x,y are real numbers with x,y≥1 then which of the following statements is always true? A) [x+y]≤[x]+[y] B) [xy]≤[x][y] C) [2x]≤2x D)[xy]≤xy
View SolutionFind graphically the solution sets of each of the following systems of inequalities :
x+y≤6
2x+5y≥−8
3x+8y≤9
10x+12y≤7
8x+7y≤14
x,y≥10
View Solution
Knowledge Check
If [] denotes the greatest integer less than or equal to the real number under consideration and −1≤x<0,0≤y<1,1≤z<2, the value of the determinant ∣∣ ∣ ∣∣[x]+1[y][z][x][y]+1[z][x][y][z]+1∣∣ ∣ ∣∣ is
A[z]B[y]C[x]DNone of theseWhich of the following to is the common region for x+y≤10,x≥5,y≤10,x≥0andy≥0.
A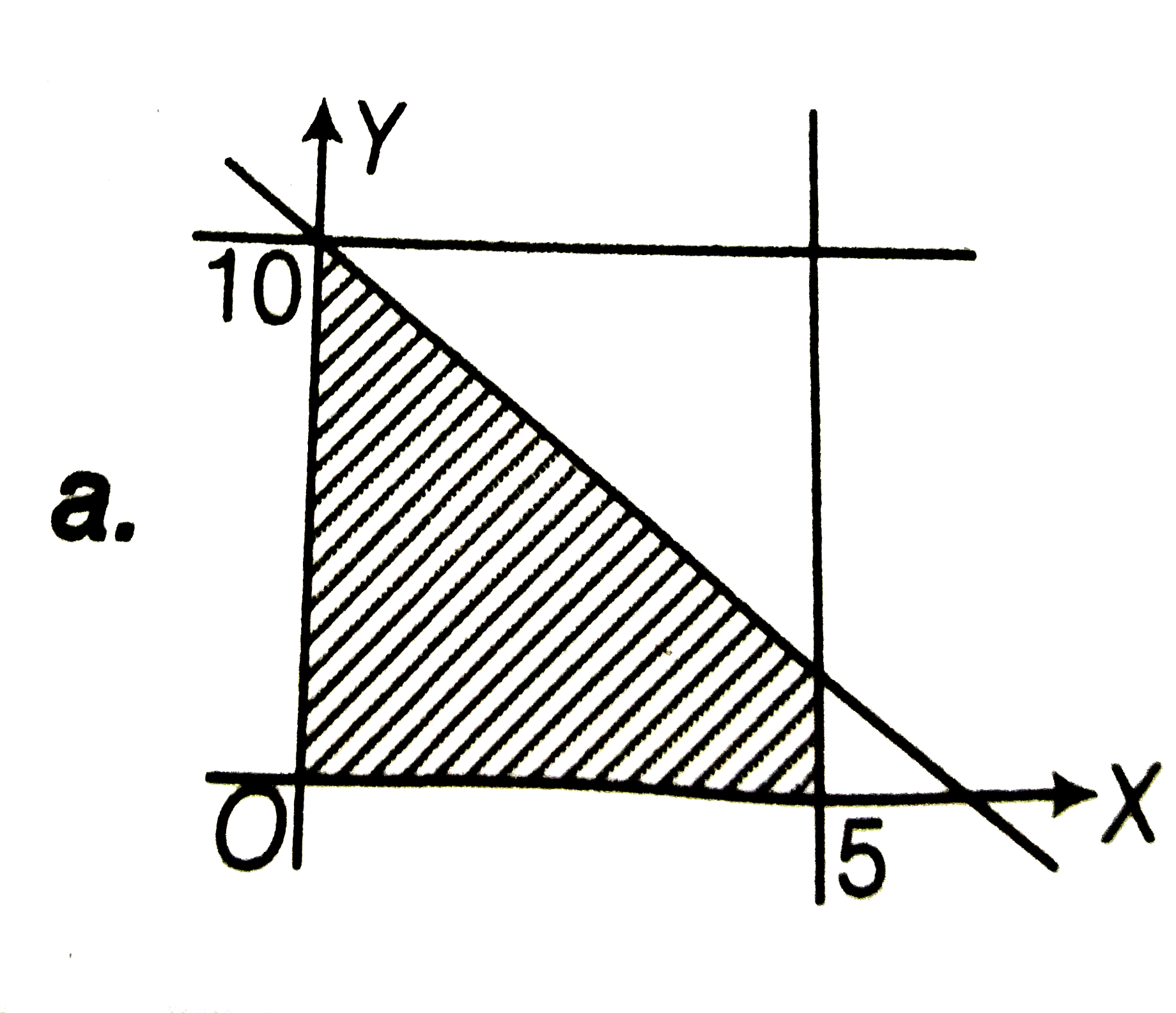 B
B C
C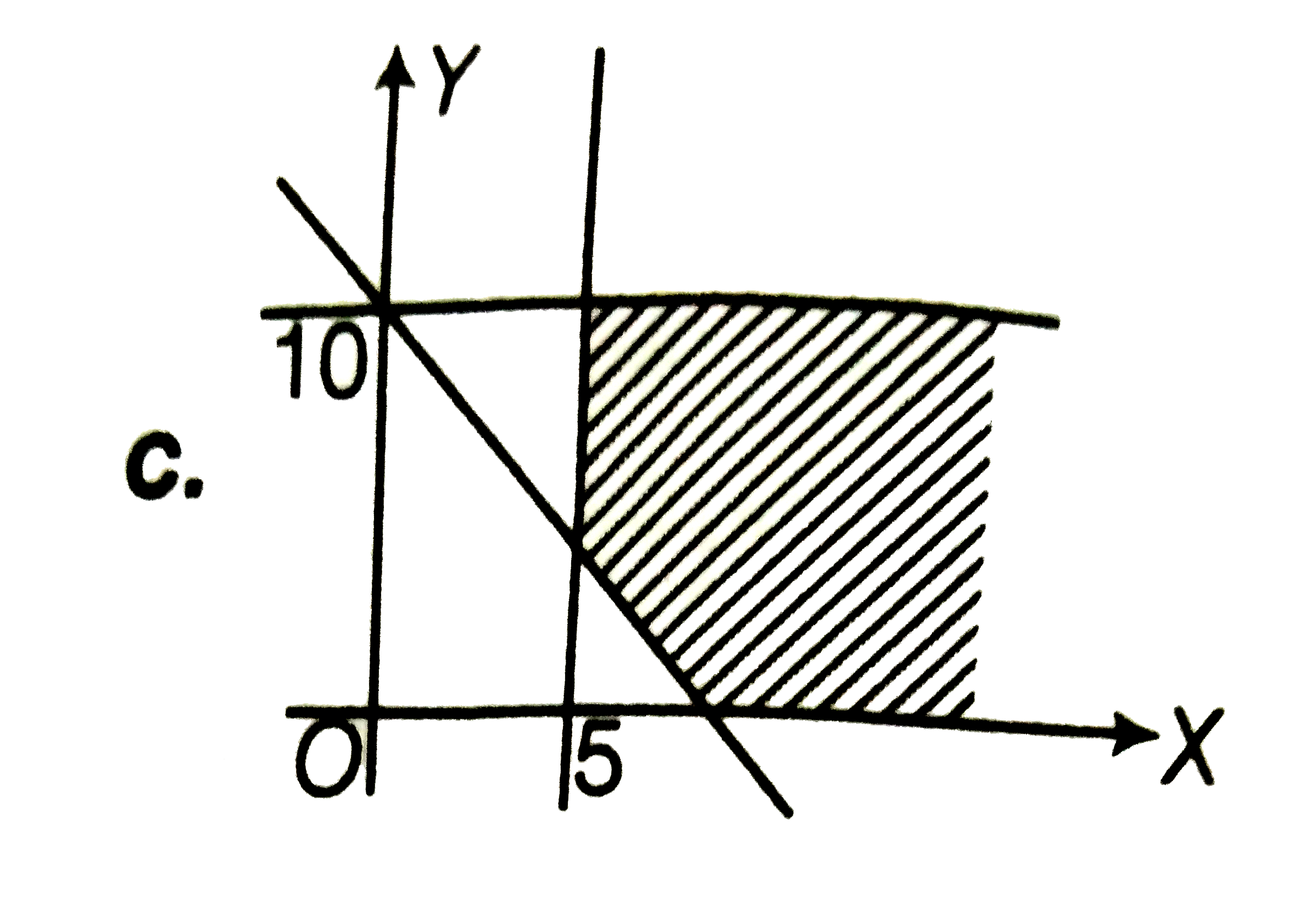 D
D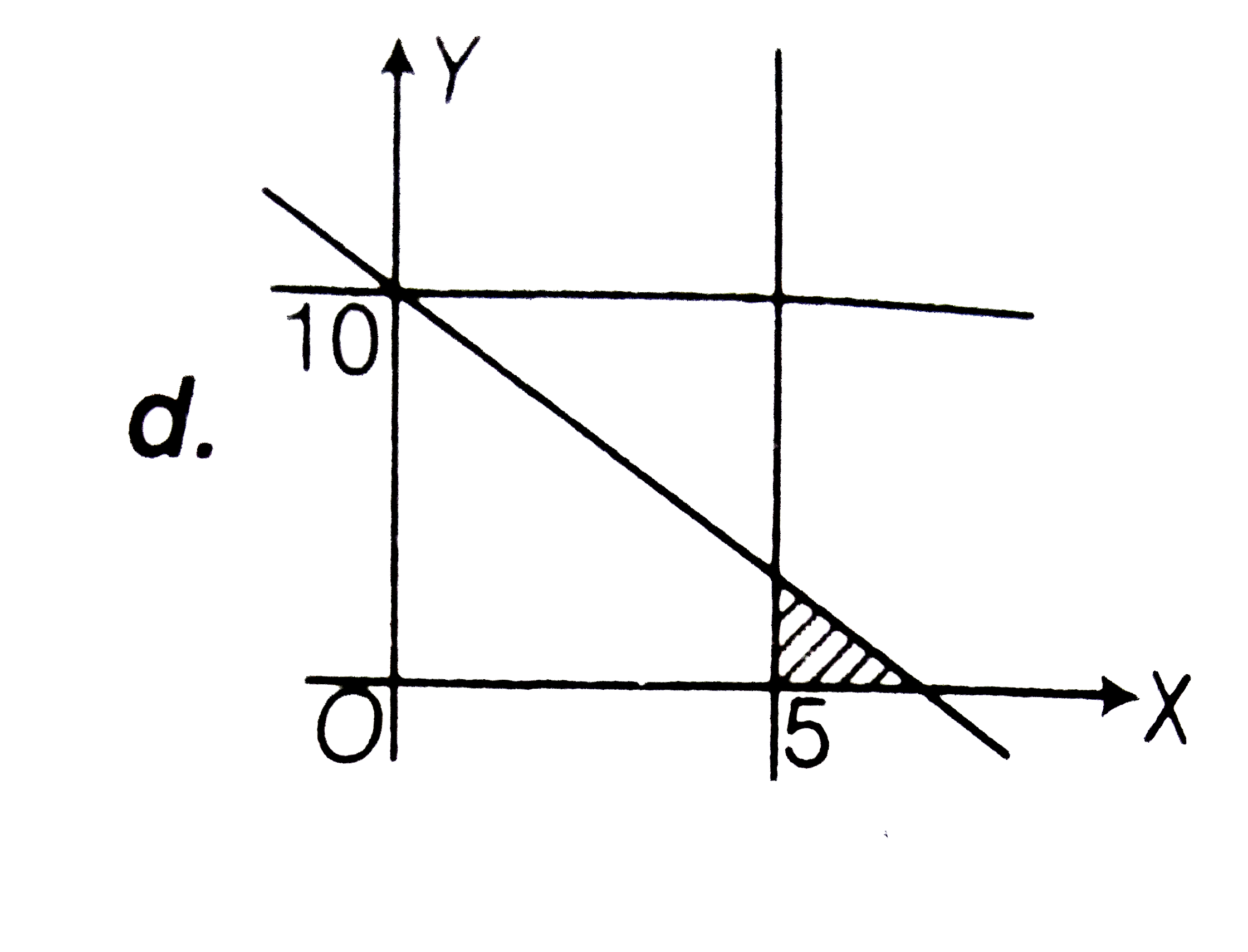
For real x with −10≤x≤10 define f(x)=∫x−102[t]dt , where for a real number r we denote by [r] the largest integer less than or equal to r. The number of points of discontinutiy of f in the interval (10,10) is
A0B10C18D19
Draw the graph of the solution set of the inequation 2x+y≥2,x−y≤1,x+2y≤8,x≥0andy≥0
View Solution2x+y≥4,x+y≤3,2x−3y≤6
View SolutionConsider a region R={(x,y)∈R2:x2≤y≤2x}. If a line y=α divides the area of region R into two equal parts, then which of the following is true.?
View SolutionThe solution of the system of equations 3x+2y≤12,x≥1,y≤2 is
View SolutionThe solution set of the inequalities 2x+y≥4,x+y≤x,2x−3y≤6 is
View Solution
