Sound waves from a tuning fork A reacha point P by two separate paths ABP and ACP. When ACP is greater than ABP by 11.5cm, there is silence at p. When the difference is 23cm the sound becomes loudest at P and 34.5cm there is silence again and so on. Calculate the minimum frequency of the fork if the velocity of sound is taken to be 331.2m/s.
The correct Answer is:1440 Hz
Given that
Δ1=11.5cm=(2n+1)λ/2
Δ1=23cm=(2n+1)λ
Δ1=34.5cm=(2n+1)3λ2
If there is no maxima or minima between Δ1,Δ2) and Δ3 that means n = 0 for maximum wavelength or minimum frequency.
λ2 = 11.5 cm
λ = 23 cm
n=vλ=331.20.23 = 1440 Hz
Topper's Solved these Questions
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Practice Exercise 6.4
10 Videos
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Practice Exercise 6.5
16 Videos
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Practice Exercise 6.2
11 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
- X-RAYSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - X-RAYSEXERCISE - Unsolved Numerica Problem for Preparation
23 Videos
Similar Questions
Sound waves from a tuning fork A reach a point P by two separate paths ABP and ACP. When ACP is greater than ABP by 11.5 cm, there is silence at P. When the difference is 23 cm the sound becomes loudest at P and when 34.5 cm there is silence again and so on. Calculate the minimum frequency of the fork if the velocity of sound is taken to be 331.2m/s.
View SolutionSound waves from a tuning fork placed at a point P reach another point Q , by two separate paths PRQandPSQ . When PSQ is greater than PRQby11.5cm , there is silence at Q . When the difference is 23cm , the sound becomes loudest at Q, and when 34.5cm , there is silence , and so on . Explain this effect and calculate the frequency of the fork if the velocity of sound is taken to be 331.2m/s.
View Solution
Knowledge Check
Sound waves from a tuning fork F reach a point P by two separate routes FAP and FBP (when FBP is greater than FAP by 12cm there is silence at P). If the difference is 24cm the the sound becomes maximum at P but at 36cm there is silence again and so on. of velocity of sound in sir is 330ms−1, then least frequency of tuning fork is :
A1537HzB1735HzC1400HzD1375HzIn an air column , resonances occurs at 25cm and 77cm. If the frequency of the fork is 325 Hz, then the velocity of sound in air will be
A364 m/sB357 m/sC338 m/sD346 m/sA piston fitted in cylindrical pipe is pulled as shown in the figure . A tuning fork is sounded at open end and loudest sound is heard at open length 13 cm, 41 cm and 69 cm, the frequency of tuning fork if velocity of sound is 350m/s is :
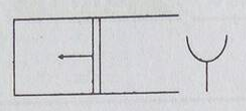 A1250 HzB625 HzC417 HzD715 Hz
A1250 HzB625 HzC417 HzD715 Hz
A sound wave of wavelength 68 cm travels 850 min 2.5 s. Calculate the frequency of the sound.
View SolutionIf the lengths of the first and second resonating air columns are 16.5cm and 51.5cm respectively with a tuning fork of frequency 512Hz, calculate the velocity of sound in air
View SolutionA tuning fork gives 15 beats per second when sounded with a sonometer wire of length 200 cm and 20 beats per second with that of length of 250 cm. calculate the frequency of the fork.
View SolutionTwo sound waves emerging from a source reach a point simultaneously along two paths. When the path difference is 12cm or 36cm, then there is a silence at that point. If the speed of sound in air be 330m/s, then calculate maximum possible frequency of the source.
View SolutionA piston fitted in cylindrical pipe is pulled as shown in the figure . A tuning fork is sounded at open end and loudest sound is heard at open length 13 cm, 41 cm and 69 cm, the frequency of tuning fork if velocity of sound is 350m/s is :

View Solution
