Question

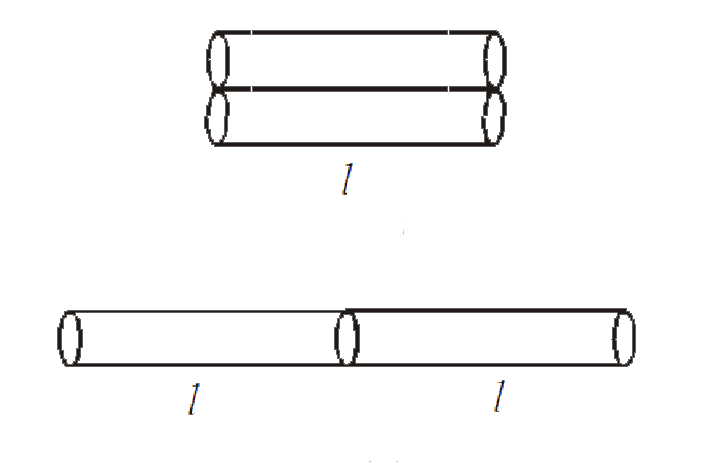
Two rods of the same length and material transfer a given amount of heat in 12 seconds when they are joined end to end. But when they are joined lengthwise, they will transfer the same amount of heat, in the same conduction, in :

Options

A. 24 s
B. 10 s
C. 15 s
D. 48 s

Answer

D

Explanation

To solve the problem, we need to analyze how heat conduction works in both configurations of the rods (end-to-end and lengthwise).

1. Understanding Heat Transfer in Rods:
The rate of heat transfer (Q) through a rod is given by the formula:
\( \frac{Q}{t} = \frac{k \cdot A \cdot \Delta T}{L} \)
where:
- \( Q \) = amount of heat transferred
- \( t \) = time taken for heat transfer
- \( k \) = thermal conductivity of the material
- \( A \) = cross-sectional area of the rod
- \( \Delta T \) = temperature difference across the rod
- \( L \) = length of the rod

2. Configuration 1: End-to-End Connection:
When the two rods are connected end-to-end, the total length becomes \( 2L \) and the area remains \( A \). The time taken to transfer heat is given as \( t = 12 \) seconds.
\( t_1 = \frac{2L}{A} \cdot \text{(constant factors)} \)
Thus, we can express the time taken as:
\( t_1 = k \cdot \frac{2L}{A \cdot \Delta T} \)
Since \( t_1 = 12 \) seconds, we have:
\( 12 = k \cdot \frac{2L}{A \cdot \Delta T} \)

3. Configuration 2: Lengthwise Connection:
When the rods are connected lengthwise, the effective length remains \( L \) for each rod, but the area is halved (assuming they have the same cross-sectional area). Therefore, the new area \( A' = \frac{A}{2} \).
The time taken in this configuration can be expressed as:
\( t_2 = \frac{L}{A/2} \cdot \text{(constant factors)} \)
This simplifies to:
\( t_2 = k \cdot \frac{L}{(A/2) \cdot \Delta T} = k \cdot \frac{2L}{A \cdot \Delta T} \)

4. Relating the Two Configurations:
From the first configuration, we have:
\( 12 = k \cdot \frac{2L}{A \cdot \Delta T} \)
From the second configuration, we have:
\( t_2 = k \cdot \frac{2L}{A \cdot \Delta T} \)
Since both expressions are equal, we can substitute:
\( t_2 = 4 \cdot t_1 \)
Therefore:
\( t_2 = 4 \cdot 12 = 48 \text{ seconds} \)

Final Answer:
The time taken to transfer the same amount of heat when the rods are joined lengthwise is 48 seconds.