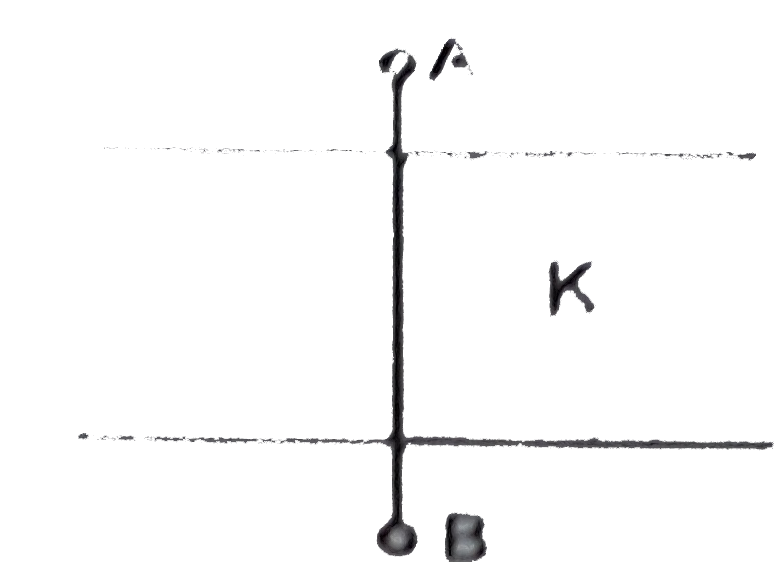
A dielectric of constant K is slipped between the plates as parallel plate condenser in half of the space as shown in the figure. If the capacity of air condenser is C, then new capacitance between A and B with be-
C2
C2K
C2[1+K]
2[1+K]C
This system is equivalent to two capacitors in parallel with area of each plate A2.
C=C1+C2
=ε0A2d+ε0AK2d
=ε0A2d[1+K]=C2[1+K]
Hence the correct answer will be (C).
Topper's Solved these Questions
Similar Questions
A dielectric of constant K is slipped between the plates of parallel plate condenser in half of the space as shown in the figure. If the capacity of air condenser is C, then new capacitance between A and B will be
c2
(B) c2K
(C) C2[1+K]
(D) 2[1+K]c

View SolutionAs shown in Fig, a dielectric material of dielectric constant K is inserted in half portion between plates of parallel plate capacitor. If its initial capacitance is C, what is the new capacitance ?

View Solution
Knowledge Check
A dielectric introduced between the plates of parallel plate condenser
Adecreases the electric field between the platesBdecreases the capacity of the condenserCincreases the charge stored in the condenserDincreases the capacity of the condenserA dielectric introduced between the plates of parallel plate condenser
Adecreases the electric field between the platesBdecreases the capacity of the condenserCincreases the charge stored in the condenserDincreases the capacity of the condenserThe capacity of a parallel plate condenser is given by
AC=QVBC=Ak∈0dCC=dAk∈0DC = A.d.
To reduce the capacity of a parallel plate condenser, separation between the plates is
View SolutionThe capacity of a parallel plate condenser is C. When the distance between the plates is halved, its capacity is
View SolutionThe separation between two plates of a parallel plate condenser is filled with two dielectric media as shown in figure . The ratio of its capacities , with and without dielectric , is

View SolutionThe distance between the plates fo a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates, what will be the new capacity ?
View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View Solution
