A charge 10 esu is placed at a distance of 2 cm from a charge 40 esu and 4 cm from another charge -20 esu. The potential energy of the charge 10 esu is : (in ergs)
87.5
112.5
150
zero
The correct Answer is:C
To find the potential energy of the charge 10esu in the presence of the other charges, we can use the formula for the potential energy U between two point charges:
U=k⋅q1⋅q2r
Where:
- U is the potential energy,
- k is the proportionality constant (in electrostatic units, k=1),
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
Step 1: Calculate the potential energy between charge 10esu and charge 40esu
Given:
- q1=10esu
- q2=40esu
- r=2cm=2×10−2m
Using the formula:
U1=1⋅10⋅402×10−2=4000.02=20000ergs
Step 2: Calculate the potential energy between charge 10esu and charge −20esu
Given:
- q1=10esu
- q2=−20esu
- r=4cm=4×10−2m
Using the formula:
U2=1⋅10⋅(−20)4×10−2=−2000.04=−5000ergs
Step 3: Calculate the total potential energy
Now, we can find the total potential energy U of the charge 10esu by adding the potential energies from both interactions:
U=U1+U2=20000ergs+(−5000ergs)=15000ergs
Final Answer
The potential energy of the charge 10esu is 15000ergs.
---
- U is the potential energy,
- k is the proportionality constant (in electrostatic units, k=1),
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
- q1=10esu
- q2=40esu
- r=2cm=2×10−2m
- q1=10esu
- q2=−20esu
- r=4cm=4×10−2m
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (A)
41 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (B) Previous Year Problems | JEE Main
30 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -1 (Objective Problems | NEET)
105 Videos
- ELECTRONICS - SEMI CONDUCTORBOOK - MOTIONCHAPTER - ELECTRONICS - SEMI CONDUCTOREXERCISE - EXERCISE - 3
29 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
13 Videos
Similar Questions
Two charges A and B of −5μC each are placed at a separation of 20 cm . Another charge C of +3 μC is placed at a separation of 20 cm from both the charges A and B . What should be the nature and magnitude of the charge to be placed at the midpoint between A and B so that net force on charge C is zero ?
View SolutionTwo identical charges, 5μC each are fixed at a distance 8 cm and a charged particle of mass 9×10−6kg and charge −10μC is placed at a distance 5 cm from each of them and is released. Find the speed of the particle when it is nearest to the two charges.
View Solution
Knowledge Check
The ratio of the emu of charge to esu of charge is :
A3×1010B4.8×10−19C1/10D1/300Two charges -4 C and +4 C are placed at 10 cm apart. The potential at the center of the line joining two charges is
A.-2 VB4 VCZeroD+2 VTwo charges q1 and q2 are placed 30cm apart, as shown in the figure. A third charge q3 is moved along the arc of a circle of radius 40cm from C to D. The change in the potential energy o fthe system is q34πε0k., where k is
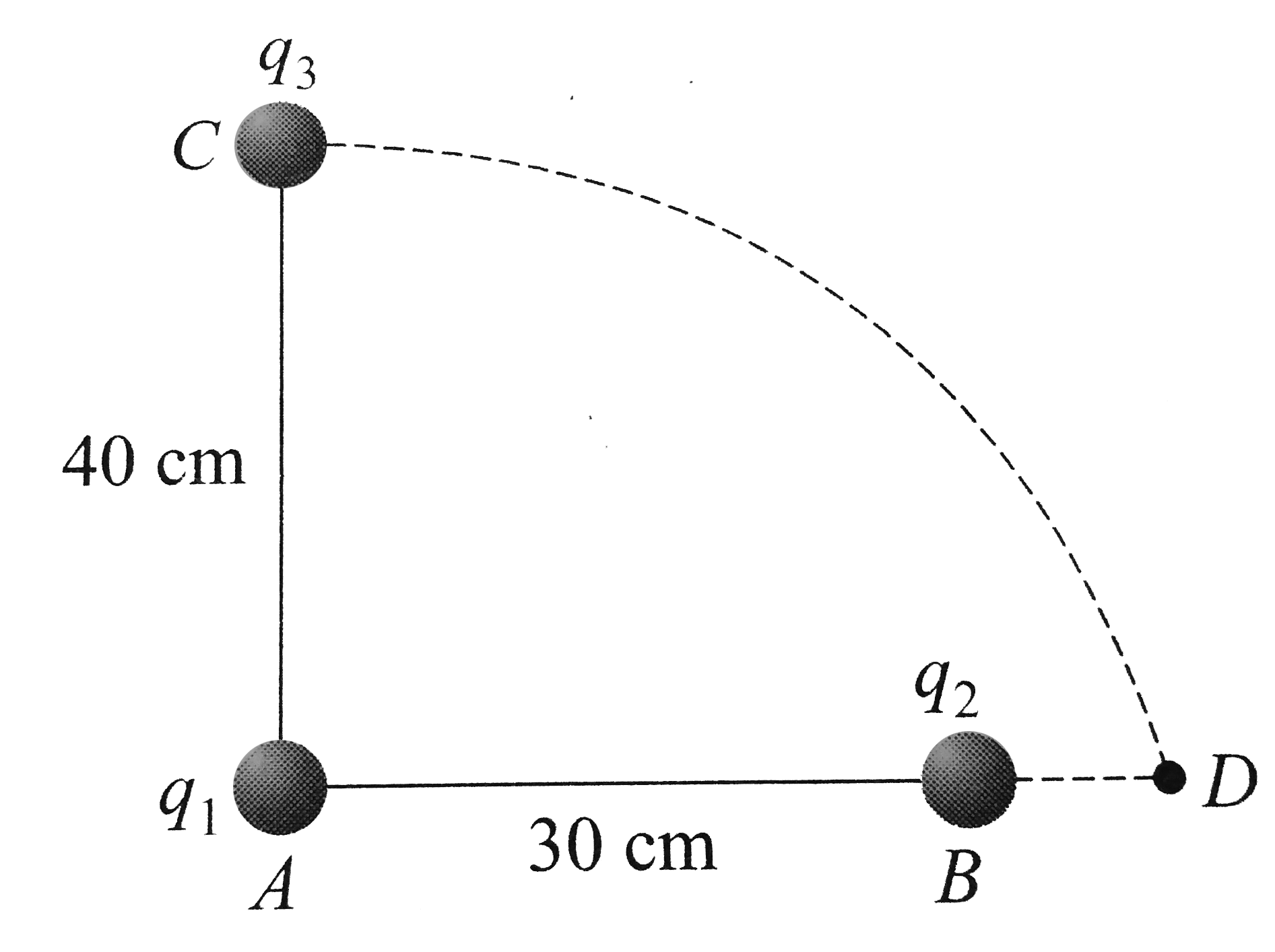 A8q1B8q1C4q1D4q1
A8q1B8q1C4q1D4q1
A point charge of 2μC is kept fixed at the origin. Another point charge of 4μC is brought from a far point to a distance of 50cm from origin. (a) Calculate the electrostatic potential energy of the two charge system. Another charge of 11μC is brought to a point 100 cm from each of the two charges. What is the work done ?
View SolutionTwo charges of values 2μC and −50μC are placed at a distance of 6 cm from each other. The distance of the point (in cm) from the bigger charge where the electric intensity will be zero is :
View SolutionTwo charged particles are placed at a distance 1.0 cm apart. What is the minimum possible magnitude of the electric force acting o each charge?
View SolutionTwo point charges 10μCand−10μC are separated by a distance of 40 cm in air.
Calculate the electrostatic potential energy of the system, assuming the zero of the potential energy to be at infinity.
View SolutionAn electric dipole consists of charges ±2.0×10−8 C separated by distance of ±2.0×10−3m. It is placed at a distance of 6 cm from a line charge of linear charge density 4.0×10−4Cm−1 as shown in figure such that the dipole makes an angle of θ=60∘ with line AB. Find the force acting on the dipole.

View Solution
