In a region where E = 0, the potential (V) varies with distance r as -
V = const. independent of (r )
The correct Answer is:D
To solve the question regarding how the electric potential (V) varies with distance (r) in a region where the electric field (E) is zero, we can follow these steps:
1. Understand the Relationship Between Electric Field and Potential:
The electric field (E) is related to the electric potential (V) by the equation:
E=−dVdr
This equation indicates that the electric field is the negative gradient of the electric potential.
2. Set the Electric Field to Zero:
In the given scenario, we know that the electric field is zero:
E=0
3. Substitute E into the Relationship:
Substituting E=0 into the equation gives:
0=−dVdr
4. Analyze the Implication of the Equation:
The equation 0=−dVdr implies that:
dVdr=0
This means that the derivative of the potential with respect to distance (r) is zero.
5. Integrate the Equation:
Since the derivative of V with respect to r is zero, it indicates that V does not change with r. Therefore, we can conclude that:
V=constant
This means that the potential V is independent of the distance r in a region where the electric field is zero.
6. Conclusion:
In a region where the electric field E=0, the potential V remains constant regardless of the distance r.
Final Answer:
The potential V varies with distance r as a constant value.
---
The electric field (E) is related to the electric potential (V) by the equation:
E=−dVdr
This equation indicates that the electric field is the negative gradient of the electric potential.
In the given scenario, we know that the electric field is zero:
E=0
Substituting E=0 into the equation gives:
0=−dVdr
The equation 0=−dVdr implies that:
dVdr=0
This means that the derivative of the potential with respect to distance (r) is zero.
Since the derivative of V with respect to r is zero, it indicates that V does not change with r. Therefore, we can conclude that:
V=constant
This means that the potential V is independent of the distance r in a region where the electric field is zero.
In a region where the electric field E=0, the potential V remains constant regardless of the distance r.
The potential V varies with distance r as a constant value.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise - 2 (Objective Problems | NEET)
64 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (A)
41 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF PRACTICE PROBLEM
27 Videos
- ELECTRONICS - SEMI CONDUCTORBOOK - MOTIONCHAPTER - ELECTRONICS - SEMI CONDUCTOREXERCISE - EXERCISE - 3
29 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
13 Videos
Similar Questions
The electric field in a region is radially outward and varies with distance r as E=250 r ( volt per square metre).Calculate the charge contained in a sphere of radius 0.2 m centeredat the origin.
View SolutionA particle of mass m moves in a circle of radius R in such a way that its speed (v) varies with distance (s) as v=a√s where a is a constant. Calcualte the acceleration and force on the particle.
View Solution
Knowledge Check
A cube of edge a is kept on x-axis in a region where electric field varies with distance as E=kxˆi. Total electric flux associated with the cube is-
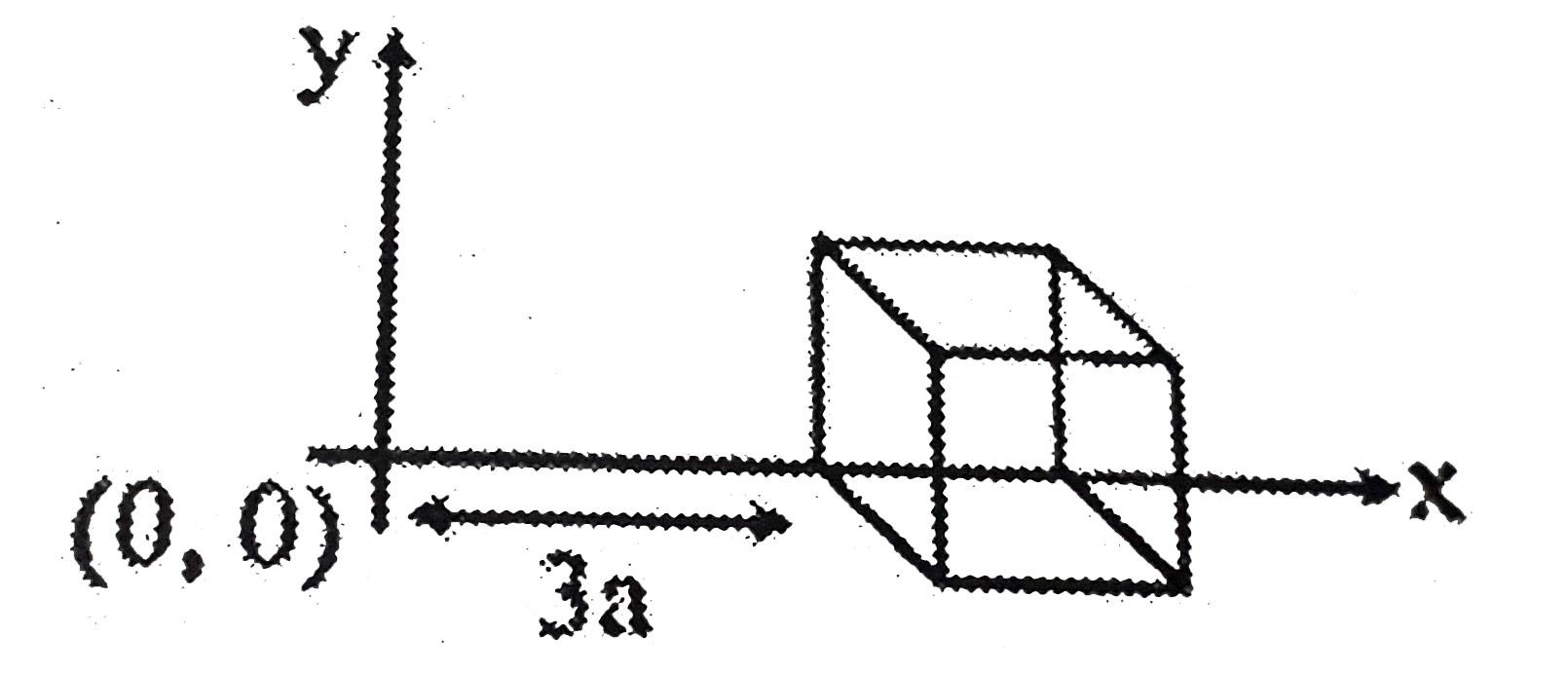 Aka3B−3ka3C4ka3Dzero
Aka3B−3ka3C4ka3DzeroA circular ring carries a uniformly distributed positive charge .The electric field(E) and potential (V) varies with distance (r ) from the centre of thr ring along its axis as
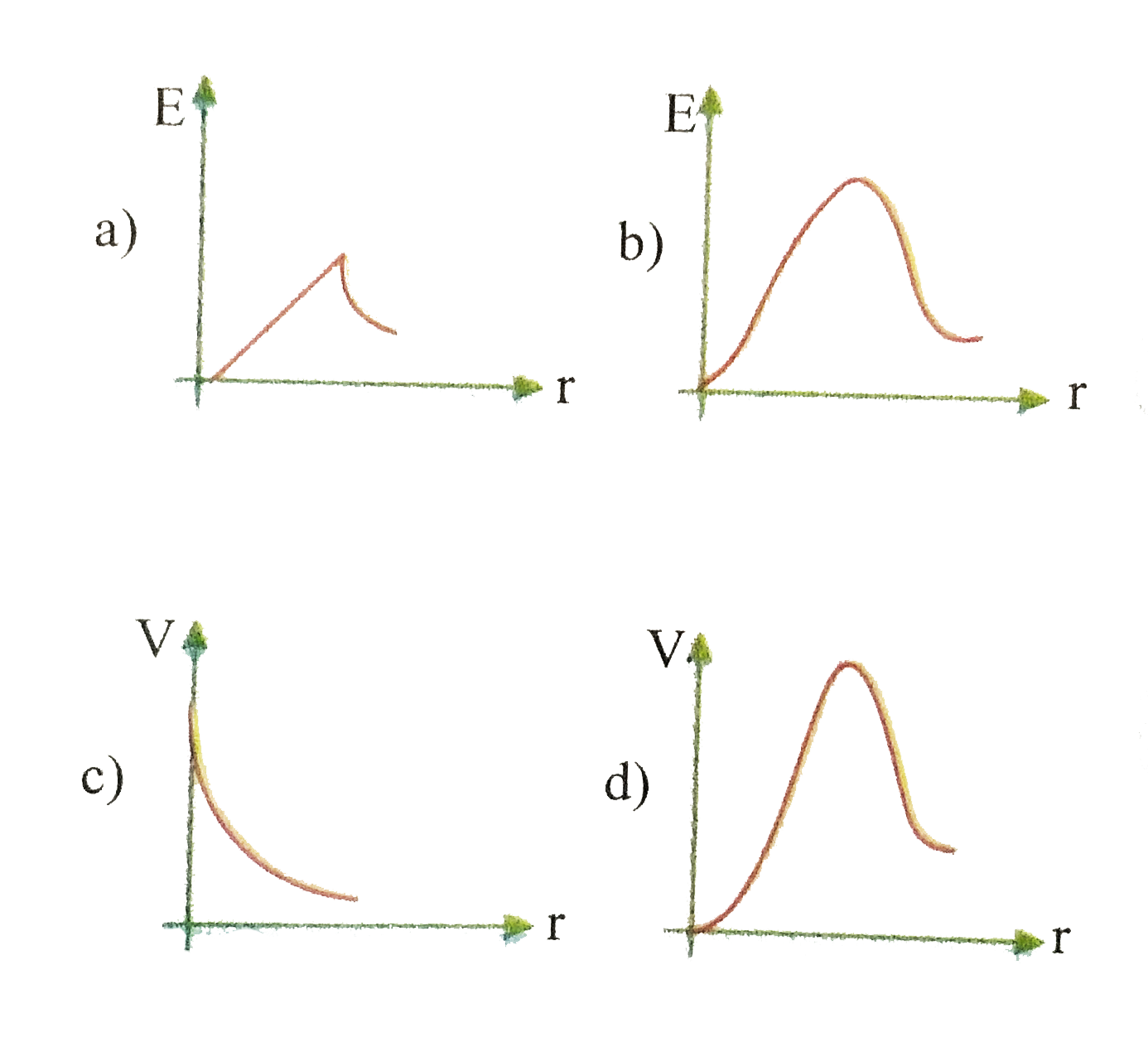 Ab andc are trueBa is trueCa,b,c are trueDa,b,c,d are true
Ab andc are trueBa is trueCa,b,c are trueDa,b,c,d are trueThe electric field is a region (relative permittivity = 1) varies with distance "r" from origin according to relation E=Ar2ˆr, where A is a positive constant. The volume charge density in the region is proportional to
ArBr2C1/rD1/r2
A particle with total energy E moves in one direction in a region where, the potential energy is U The acceleration of the particle is zero, where,
View SolutionThe electric field and the potential of an electric dipole vary with distance 'r' as
View SolutionThe electric field and the potential of an electric dipole vary with distance r as
View SolutionIn a spherical region the densiy varies inversely with the distance from ther centre Gravitational field at a distance r from the centre is .
View SolutionAccording to C.E. van der Waal, the interatomic potential varies with the average interatomic distance (R) as
View Solution
