If an isollated infinite sheet contains charge $Q_{1}$ on its one surface and charge $Q_{2}$ on its other surface, then prove that electric field intensity at a point in front of sheet will be $\frac{Q}{2 A ε_{0}}$ , where $Q = Q_{1} + Q_{2}$

Video Solution

Text Solution

Verified by Experts

Electric field at point P :
$\vec{E} = {\vec{E}}_{Q_{1}} + {\vec{E}}_{Q_{2}}$

$= \frac{Q_{1}}{2 A ε_{0}} \hat{n} + \frac{Q_{2}}{2 A ε_{0}} \hat{n}$
$= \frac{Q_{1} + Q_{2}}{2 A ε_{0}} \hat{n} = \frac{Q}{2 A ε_{0}} \hat{n}$
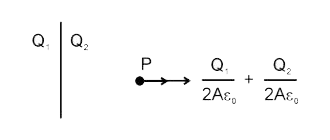
[This shows that the resultant field due to sheet depends only on the total charge of the sheet and not on the distribution of charge on individual surfaces].

Updated on:21/07/2023

If q is the charge per unit area on the surface of a conductor, then the electric field intensity at a point on the surface is
A $(\frac{q}{ε_{0}})$ normal to surface
B $(\frac{q}{2 ε_{0}})$ normal to surface
C $(\frac{q}{ε_{0}})$ tangential to surface
D $(\frac{q}{2 ε_{0}})$ tangential to surface
Charges $+ 2 Q$ and $- Q$ are placed as shown in figure. The point at which electric field intensity is zero will be

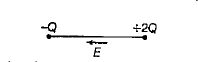ASomewhere between $- Q$ and $+ 20$
BSomewhere on the left of $- Q$
CSomewhere on the right of $+ 2 Q$
DSomewhere on the right bisector of line Joining $- Q$ and $+ 2 Q$
Charge $2 q and - q$ are placed at $(a, 0) and (- a, 0)$ as shown in the figure. The coordinates of the point at which electric field intensity is zero will be $(x, 0)$ where

A $- a < x < a$
B $x < - a$
C $x > - a$
D $0 < x < a$