A block having mass m and charge Q is resting on a frictionless plane at a distance d from fixed large non-conducting infinite sheet of uniform charge density −σ as shown in Figure. Assuming that collision of the block with the sheet is perfectly elastic, find the time period of oscillatory motion of the block. Is it SHM ?
The situation is shown in figure. Electric force produced by sheet will accelerate the block towards the sheet producing an acceleration. Acceleration will be uniform because electric field E due to the sheet is uniform.
a=Fm=qEm, where E=σ/2ε0

As initially the block is at rest and acceleration is constant, from second equation of motion, time taken by the block to each the wall
L=12at2
i.e., t=√2La=√2mLaE=√4mLε0aσ
As collision with the is perfectly elastic, the block will rebound with same speed and as now its motion is opposite to the acceleration, it will come to rest after travelling same distance L in same time t. After stopping it will be again accelerated towards the wall and so the block will execute oscillatory motion with 'span' L and time period.
T=2t=2√2mLaE=2√4mLε0aσ
However, as the restoring force F = qE is constant and not proportional to displacement x, the motion is not simple harmonic.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF MISCELLANEOUS PROBLEM (Example )
15 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF PRACTICE PROBLEM
27 Videos
- ELECTRONICS - SEMI CONDUCTORBOOK - MOTIONCHAPTER - ELECTRONICS - SEMI CONDUCTOREXERCISE - EXERCISE - 3
29 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
13 Videos
Similar Questions
A block having mass 'm' ad carge q is resting on a fractionless plane at distance L from the wall as shown in fig.Discuss the motion of the block when a uniform electric field E is applied horizontally towards the wall assuming that collision of the block with the wall is perfectly elastic.
View SolutionFind out energy stored in an imaginary cubical volume of side a in front of a infinitely large non-conducting sheet of uniform charge density σ.
View Solution
Knowledge Check
A charge +q is situated at a distance 'd' away from both the sides of a grounded conducting 'L' shaped sheet as shown in the figure.
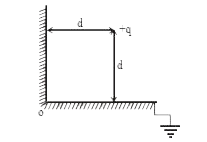
The force acting on the charge +q isAtowards O, magnitude q232πε0d2(2√2+1)Baway from O, magnitude q232πε0d2(2√2+1)Ctowards O, magnitude q232πε0d2(2√2−1)Daway from O, magnitude q232πε0d2(2√2−1)A block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression 2x0 an block is released from rest. Collision with the wall PQ are elastic.
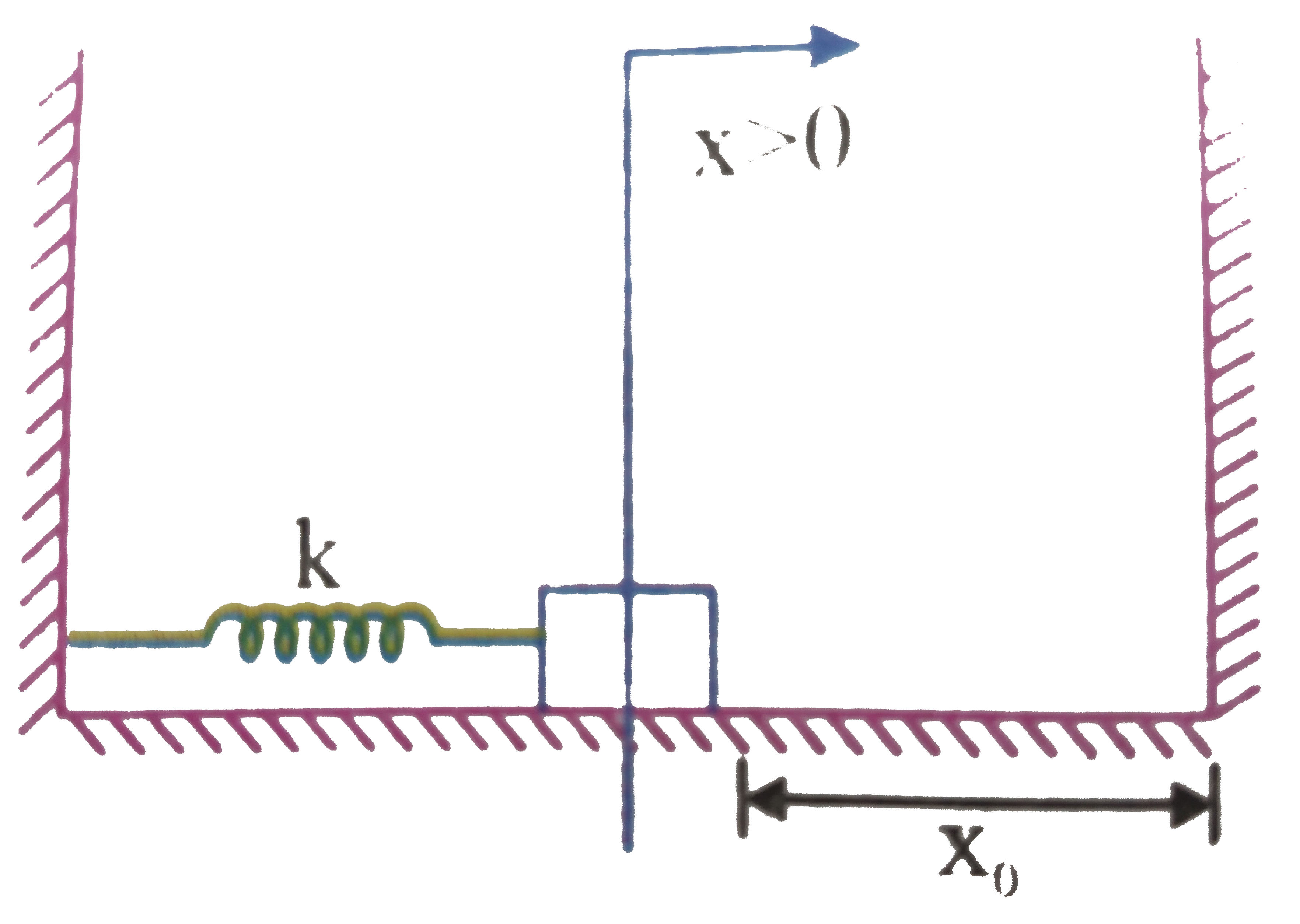
Find the time period of motion of the block:A2π3√mkB4π3√mkC3π2√mkDπ2√mk
Electric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionA particle of mass M and negative charge q is thrown in a gravity free space with speedd u from the point A on the large non conducting charged sheet with surface charge density (sigma), as shown in figure, Find the maximum distance from A on sheet where the rparticle can strike .

View SolutionFigure shown a block P of mass m resting on a smooth horizontal surface, attached to a spring of force constant k which is rigidly fixed on the wall on left side, shown in the figure . At a distance l to the right of the block there is a rigid wall. If block is pushed towards loft so that spring is compressed by a distance 5l/3 and when released, if will starts its oscillations. If collision of block with the wall is considered to be perfectly elastic. Find the time period of oscillation of the block.

View SolutionTwo infinite non-conducting sheets each with uniform surface charge density sigma are kept in such a way that the angle between them is 30^(@). The electric field in the region I shown between them is
View SolutionA cube of edge a is placed at some distance from a long plane sheet of charge having surface density σ. Find the electric energy stored in the cube.
View SolutionIf three infinite charged sheets of uniform surface charge densities σ,2σ and −4σ are placed as shown in figure, then find out electric field intensities at points A, B, C and D.

View Solution
