Conducting wire of parabolic shape, initially $y = x^{2}$ is moving with velocity $\to V = v_{0} ˆ i$ in a non-uniform magnetic field $\to B = B_{0} (1 + {(\frac{y}{L})}^{β}) ˆ k$ as shown in figure. If $V_{0}, B_{0} L$ and B are +ve constant $Δ ϕ$ is potential difference develop between the ends of wire, then correct statements (s) is/are

$| Δ ϕ |$ remains the same if the parabolic wire is replaced by a straight wire, $y = x$ initially, of length $\sqrt{2} L$

$| Δ ϕ | = \frac{1}{2} B_{0} V_{0} L for β = 0$
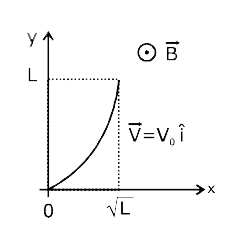
ocr_image

$| Δ ϕ |$ is proportional to the length of the wire projected on the y-axis.

$| Δ ϕ | = \frac{4}{3} B_{0} V_{0} L for β = 2$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C, D

Answer

Step by step video, text & image solution for Conducting wire of parabolic shape, initially y=x^(2) is moving with velocity vec(V)=v_(0) hati in a non-uniform magnetic field vec(B)=B_(0)(1+(y/L)^(beta))hatk as shown in figure. If V_(0) , B_(0) L and B are +ve constant Deltaphi is potential difference develop between the ends of wire, then correct statements (s) is/are by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS MAGNETISM AND MATTER

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A proton is fired from origin with velocity $\to v = v_{0} ˆ j + v_{0} ˆ k$ in a uniform magnetic field $\to B = B_{0} ˆ j$ .
Aits z-coordinate can never be negative
Bits x-coordinate can never be negative
Cits x-and z-coordinates cannot be zero at the same time
Dits y-coordinate will be proportional to its time of flight
Question 2 - Select One
An electron is moving with an initial velocity $\to v = v_{0} ˆ i$ and is in a magnetic field $\to B = B_{0} ˆ j$ . Then it's de-Broglie wavelength
Aremains constant
Bincreases with time
Cdecreases with time
Dincreases and decreases periodically
Question 3 - Select One or More
A portion is fired from origin with velocity $\to v = v_{0} ˆ j + v_{0} ˆ k$ in a uniform magnetic field $\to B = B_{0} ˆ j$ . In the subsequent motion of the proton
Aits z co-ordinate can never be negative
Bits x co-ordinate can never be positive
Cits x and z co-oridinate cannot be zero at the same time
Dits y co-ordinate will be proportional to its time of flight

MOTION-MAGNETISM -EXERCISE-4 (LEVEL-II)

Home
Ask Doubt
Profile

Conducting wire of parabolic shape, initially y=x2 is moving with velocity →V=v0ˆi in a non-uniform magnetic field →B=B0(1+(yL)β)ˆk as shown in figure. If V0,B0L and B are +ve constant Δϕ is potential difference develop between the ends of wire, then correct statements (s) is/are

The correct Answer is:A, C, D

Topper's Solved these Questions

Similar Questions

Knowledge Check

A proton is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj.

An electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=B0ˆj. Then it's de-Broglie wavelength

A portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton

MOTION-MAGNETISM -EXERCISE-4 (LEVEL-II)

A proton is fired from origin with velocity $\to v = v_{0} ˆ j + v_{0} ˆ k$ in a uniform magnetic field $\to B = B_{0} ˆ j$ .

An electron is moving with an initial velocity $\to v = v_{0} ˆ i$ and is in a magnetic field $\to B = B_{0} ˆ j$ . Then it's de-Broglie wavelength

A portion is fired from origin with velocity $\to v = v_{0} ˆ j + v_{0} ˆ k$ in a uniform magnetic field $\to B = B_{0} ˆ j$ . In the subsequent motion of the proton