A ray of light of refractive index $1.4$ approaches the boundary surface between the liquids and air at an angle of incidence whose sine is $0.8$ .Which of the following statements is correct about the behaviour of the light

It is impossible to predict the behavior of the light ray on the basis of the information supplied

The sine of the angle of refraction of the emergent ray will less than 0.8

The ray will be internally reflected

The sine of the angle of refraction of the emergent ray will be greater than 0.8.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Answer

Step by step video & text solution for A ray of light of refractive index 1.4approaches the boundary surface between the liquids and air at an angle of incidence whose sine is 0.8.Which of the following statements is correct about the behaviour of the light by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRUMENTS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A ray of light travelling in transparent medium of refractive index $μ$ falls on a surface separating the medium from air at an angle of incidence of $45^{\circ}$ . For which of the following value of $μ$ the ray can undergo total internal reflection ?
A $μ > 1.33$
B $μ > 1.4$
C $μ > 1.5$
D $μ > 1.25$
Question 2 - Select One
A ray of light travelling in a transparent medium f refractive index $μ$ , falls on a surface separating the medium from air at an angle of incidence of $45^{\circ}$ . For which of the following value of $μ$ the ray can undergo total internal reflection ?
A $μ = 1.33$
B $μ = 1.40$
C $μ = 1.50$
D $μ = 1.25$
Question 3 - Select One
Figure, a light ray is incident on the lower medium boundary at an angle if $45^{\circ}$ with the normal. Which of the following statement $i s / a r e$ true?

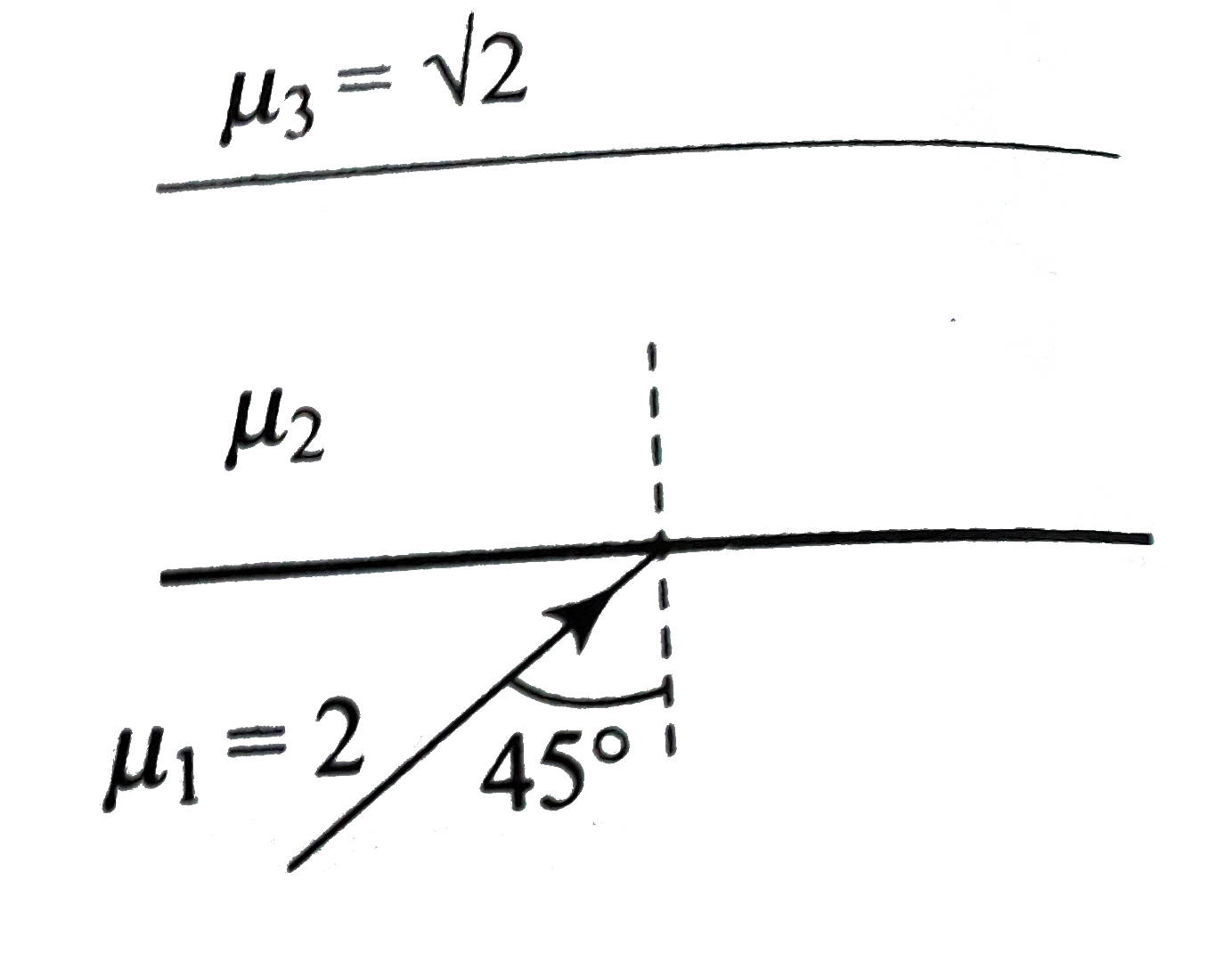AIf $μ_{2} > \sqrt{2}$ , then angle of deviation is $45^{\circ}$
BIf $μ_{2} < \sqrt{2}$ , then angle of deviation is $90^{\circ}$
CIf $μ_{2} < \sqrt{2}$ , then angle of deviation is $135^{\circ}$
DIf $μ_{2} > \sqrt{2}$ , then angle of deviation is $0^{\circ}$

MOTION-GEOMETRICAL OPTICS-Exercise - 2 (Level-I)

Home
Ask Doubt
Profile

A ray of light of refractive index 1.4approaches the boundary surface between the liquids and air at an angle of incidence whose sine is 0.8.Which of the following statements is correct about the behaviour of the light

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

A ray of light travelling in transparent medium of refractive indexμfalls on a surface separating the medium from air at an angle of incidence of 45∘. For which of the following value of μthe ray can undergo total internal reflection ?

A ray of light travelling in a transparent medium f refractive index μ, falls on a surface separating the medium from air at an angle of incidence of 45∘. For which of the following value of μ the ray can undergo total internal reflection ?

Figure, a light ray is incident on the lower medium boundary at an angle if 45∘ with the normal. Which of the following statement is/are true?

MOTION-GEOMETRICAL OPTICS-Exercise - 2 (Level-I)

A ray of light of refractive index $1.4$ approaches the boundary surface between the liquids and air at an angle of incidence whose sine is $0.8$ .Which of the following statements is correct about the behaviour of the light

A ray of light travelling in transparent medium of refractive index $μ$ falls on a surface separating the medium from air at an angle of incidence of $45^{\circ}$ . For which of the following value of $μ$ the ray can undergo total internal reflection ?

A ray of light travelling in a transparent medium f refractive index $μ$ , falls on a surface separating the medium from air at an angle of incidence of $45^{\circ}$ . For which of the following value of $μ$ the ray can undergo total internal reflection ?

Figure, a light ray is incident on the lower medium boundary at an angle if $45^{\circ}$ with the normal. Which of the following statement $i s / a r e$ true?