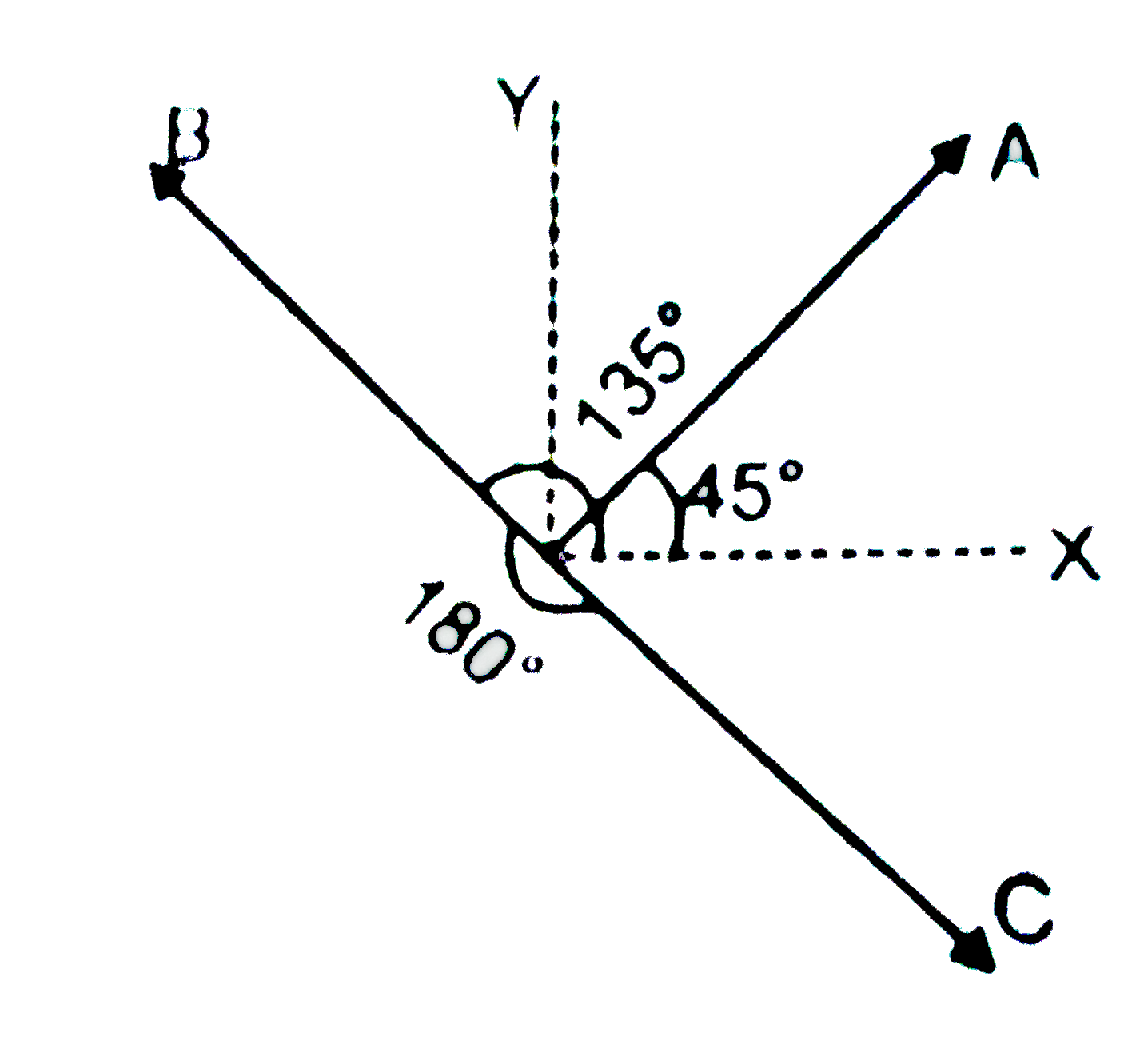
Add vectors $\to A, \to B and \to C$ each having magnitude of 100 unit and inclined to the X-axis at angles $45^{\circ}, 135^{\circ} and 315^{\circ}$ respectively.

Video Solution

Text Solution

Verified by Experts

$| R | = 100$ unit inclined at $45^{\circ}$ to the x-axis

|

Updated on:21/07/2023

Class 12 PHYSICS BASIC MATHEMATICS & VECTORS

Similar Questions

Add vectors $\to A, \to B$ and $\to C$ which have equal magnitude s of 50 unit and are inclined at angles of $45^{\circ}, 135^{\circ}$ and $315^{\circ}$ respectively from x-axos.

View Solution
Let $\to A and \to B$ be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angles $30^{\circ} and 60^{\circ}$ respectively, find the resultant.
View Solution

Knowledge Check

Question 1 - Select One
If $\to a and \to b$ are unit vectors inclined to x-axis at angle $30^{\circ} and 120^{\circ}$ then $∣ ∣ \to a + \to b ∣ ∣$ equals
A $\sqrt{2 / 3}$
B $\sqrt{2}$
C $\sqrt{3}$
D2
Question 2 - Select One
The vector sum of three vectors $\to A, \to B$ and $\to C$ is zero . If $ˆ i$ and $ˆ j$ are the unit vectores in the vectors in the directions of $\to A$ and $\to B$ respectively , them :
A $\to C$ is in the plane of $ˆ i$ of $ˆ j$
B $\to C$ is along $ˆ i \times ˆ j$
C $\to C$ is along $ˆ i$
D $\to C$ is along $ˆ j$
Question 3 - Select One
A magnitude of vector $\to A, \to B$ and $\to C$ are respectively $12, 5$ and $13$ units and $\to A + \to B = \to C$ then the angle between $\to A$ and $\to B$ is
A $0$
B $π$
C $π / 2$
D $π / 4$

Recommended Questions

Home
Ask Doubt
Profile