A disc rotated about its central axis and gently placed on another coaxial disc at rest. Due to friction between the two first disc retards and the second one starts rotating and after some time both with rotate with a common angular speed. In this process the total internal energy of the system of two discs does not change. State and justify whether this statement is true or false.
To determine whether the statement "the total internal energy of the system of two discs does not change" is true or false, we can analyze the situation step by step.
1. Understanding the System:
- We have two discs: one is rotating with an initial angular speed (ω) and the other is at rest.
- When the rotating disc is placed on the stationary disc, friction between them will cause the rotating disc to slow down and the stationary disc to start rotating.
2. Angular Momentum Conservation:
- Since there are no external torques acting on the system, the angular momentum of the system is conserved.
- Let the moment of inertia of each disc be I. The initial angular momentum of the system is:
Linitial=I⋅ω+0=I⋅ω
- After some time, both discs rotate together with a common angular speed ω′. The final angular momentum is:
Lfinal=(I+I)⋅ω′=2I⋅ω′
- Setting the initial and final angular momentum equal gives:
I⋅ω=2I⋅ω′
- From this, we can solve for ω′:
ω′=ω2
3. Kinetic Energy Calculation:
- The initial kinetic energy of the rotating disc is:
KEinitial=12Iω2
- The kinetic energy of the stationary disc is zero:
KEinitial, stationary=0
- Therefore, the total initial kinetic energy of the system is:
KEtotal initial=12Iω2+0=12Iω2
- After both discs start rotating together, the total kinetic energy becomes:
KEtotal final=12(I+I)(ω2)2=12(2I)(ω24)=Iω24
4. Change in Kinetic Energy:
- The change in kinetic energy of the system is:
ΔKE=KEtotal final−KEtotal initial=Iω24−12Iω2=Iω24−2Iω24=−Iω24
- This shows that the total kinetic energy of the system has decreased.
5. Conclusion:
- Since the kinetic energy of the system has decreased, the statement that "the total internal energy of the system of two discs does not change" is false.
- We have two discs: one is rotating with an initial angular speed (ω) and the other is at rest.
- When the rotating disc is placed on the stationary disc, friction between them will cause the rotating disc to slow down and the stationary disc to start rotating.
- Since there are no external torques acting on the system, the angular momentum of the system is conserved.
- Let the moment of inertia of each disc be I. The initial angular momentum of the system is:
Linitial=I⋅ω+0=I⋅ω
- After some time, both discs rotate together with a common angular speed ω′. The final angular momentum is:
Lfinal=(I+I)⋅ω′=2I⋅ω′
- Setting the initial and final angular momentum equal gives:
I⋅ω=2I⋅ω′
- From this, we can solve for ω′:
ω′=ω2
- The initial kinetic energy of the rotating disc is:
KEinitial=12Iω2
- The kinetic energy of the stationary disc is zero:
KEinitial, stationary=0
- Therefore, the total initial kinetic energy of the system is:
KEtotal initial=12Iω2+0=12Iω2
- After both discs start rotating together, the total kinetic energy becomes:
KEtotal final=12(I+I)(ω2)2=12(2I)(ω24)=Iω24
- The change in kinetic energy of the system is:
ΔKE=KEtotal final−KEtotal initial=Iω24−12Iω2=Iω24−2Iω24=−Iω24
- This shows that the total kinetic energy of the system has decreased.
- Since the kinetic energy of the system has decreased, the statement that "the total internal energy of the system of two discs does not change" is false.
Topper's Solved these Questions
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Conceptual MCQs Single Option Correct
21 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Numerical MCQs Single Options Correct
42 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Practice Exercise 3.4
11 Videos
- PHOTOELECTRIC EFFECT AND MATTER WAVESBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - PHOTOELECTRIC EFFECT AND MATTER WAVESEXERCISE - Unsolved numerical problems
42 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
Similar Questions
Two coaxial discs rotating in the same sense, stick to each other and spin with common angular speed. Find the loss in kinetic energy of the system?
View SolutionA disc rotates about its axis with a constant angular acceleration of 4rads2. Find the radia and tangential acceleration of a particle at a distance of 1 cm from the axis at the end of the first second after the disc starts rotating.
View Solution
Knowledge Check
A horizontal disc rotates freely about a vertical axis through its centre. A ring, having the same mass and radius as the disc, is now gently placed on the disc. After some time, the two rotate with a common angular velocity, then
Asome friction exists between the disc and the ringBthe angular momentum of the 'disc plus ring' is conservedCthe final common angular velocity is (23)rd of the initial angular velocity of the discD(23)rd of the initial kinetic energy changes to heatA horizontal disc rotates freely with angular velocity ω about a vertical axes through its centre. A rig having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.
Ano friction exists between te disc and the ringBthe angular momentum of the system is conservedCthe final common angular velocity is 12ωDall of the above
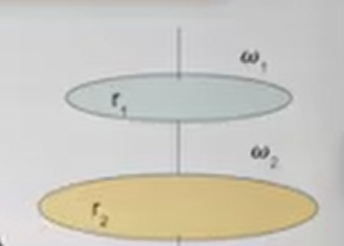
Two identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity ω0 and has rotational kinetic energy K0. Change in the rotational kinetic energy of the system isAK0/2B−K0/2C−K0/4DK0/4
A circular disc of moment of inertia It is rotating in a horizontal plane about its symmetry axis with a constant angular velocity ωi. Another disc of moment of inertia Ib is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed ωf. Calculate the energy lost by the initially rotating disc due to friction.
View SolutionA disc with moment of inertial I is rotating with some angular speed. Second disc is initially at rest. Now second disc with moment of inertia 3I is placed on first disc and starts rotating. Find loss of kinetic energy in fraction
View SolutionA disc, initially at rest, starts rotating about its own axis/ with a constant angular acceleration of 0*2 rad/s2. The time taken by the disc to rotate by 10 rad (in seconds) is
View SolutionA uniform circulr disc of mass 200 g and radius 4.0 cm is rotated about one of its diameter at an angular speed of 10 rad/s. Find the knetic energy of the disc and its angular momentum about the axis of rotation.
View SolutionA disc initially at rest , is rotated about its axis with uniform angular acceleration . In the first 2 s, it rotates an angle θ . In the next 2s, the disc rotates through an angle
View Solution
