If coefficient of static friction is μs and coefficient of kinetic friction is μk , which one is correct ?
μs=μk
μs>μk
μs<μk
μs≤μk
The correct Answer is:B
To solve the question regarding the relationship between the coefficient of static friction (µs) and the coefficient of kinetic friction (µk), we can follow these steps:
1. Understanding Static and Kinetic Friction:
- Static Friction (Fs): This is the frictional force that prevents an object from starting to move. It acts when the object is at rest and a force is applied to it. The maximum static friction force is given by Fs,max=μs⋅N, where N is the normal force.
- Kinetic Friction (Fk): This is the frictional force acting on an object that is already in motion. The kinetic friction force is given by Fk=μk⋅N.
2. Comparing the Two Coefficients:
- It is generally observed that the coefficient of static friction (µs) is greater than the coefficient of kinetic friction (µk). This means that it takes more force to start moving an object than to keep it moving once it has started.
3. Mathematical Representation:
- From the definitions, we can write:
- For static friction: Fs,max=μs⋅N
- For kinetic friction: Fk=μk⋅N
- Since Fs,max is the maximum force before motion begins, and Fk is the force during motion, we conclude that:
μs>μk
4. Conclusion:
- Therefore, the correct statement is that the coefficient of static friction (µs) is greater than the coefficient of kinetic friction (µk). Thus, we can conclude:
μs>μk
- Static Friction (Fs): This is the frictional force that prevents an object from starting to move. It acts when the object is at rest and a force is applied to it. The maximum static friction force is given by Fs,max=μs⋅N, where N is the normal force.
- Kinetic Friction (Fk): This is the frictional force acting on an object that is already in motion. The kinetic friction force is given by Fk=μk⋅N.
- It is generally observed that the coefficient of static friction (µs) is greater than the coefficient of kinetic friction (µk). This means that it takes more force to start moving an object than to keep it moving once it has started.
- From the definitions, we can write:
- For static friction: Fs,max=μs⋅N
- For kinetic friction: Fk=μk⋅N
- Since Fs,max is the maximum force before motion begins, and Fk is the force during motion, we conclude that:
μs>μk
- Therefore, the correct statement is that the coefficient of static friction (µs) is greater than the coefficient of kinetic friction (µk). Thus, we can conclude:
μs>μk
Similar Questions
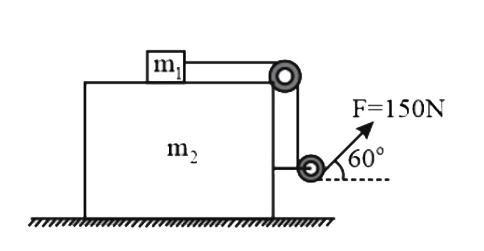
In the arrangement shown in the figure, friction exists only between the two blocks, A and B. The coefficient of static friction μs=0.6 and coefficient of kinetic friction μk=0.4, the masses of the blocks A and B are m1=20kg and m2=30kg, respectively. Find the acceleration (in ms−2) of m1, if a force F=150N is applied, as shown in the figure. [Assume that string and pulleys are massless]
View SolutionA body of mass 10 kg is kept on a horizontal floor of coefficient of static friction μs=0.5 and coefficient of kinetic friction μk=0.45 as shown in figure.
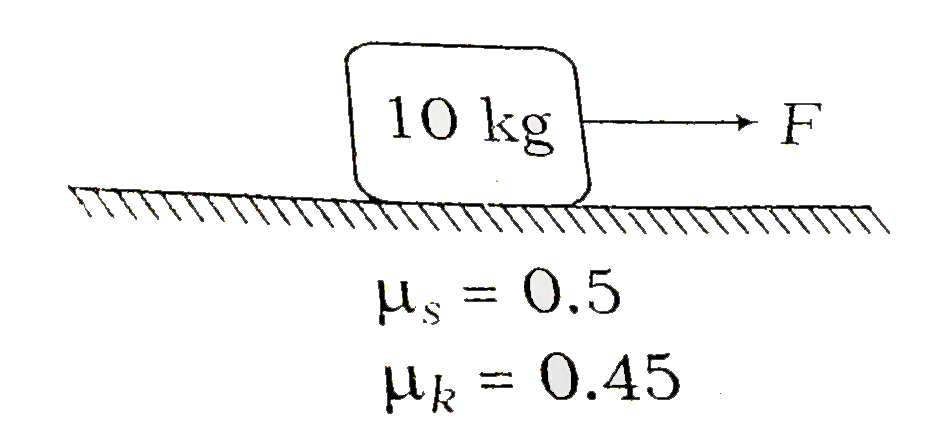
Find the acceleration, force of friction and contact force on the body by the plane when the driving force is (g=10ms−2)
(i) 40 N (ii)60N
View Solution
Knowledge Check
A block A kept on a rough plate (OOI) with coefficient of static friction μs=0.75 & coefficient of kinetic friction μˆk=0.5. The plate is leaning with horizontal at an angle θ=tan−1(μ's). If the plate is further tilted slightly then the acceleration of block will be :
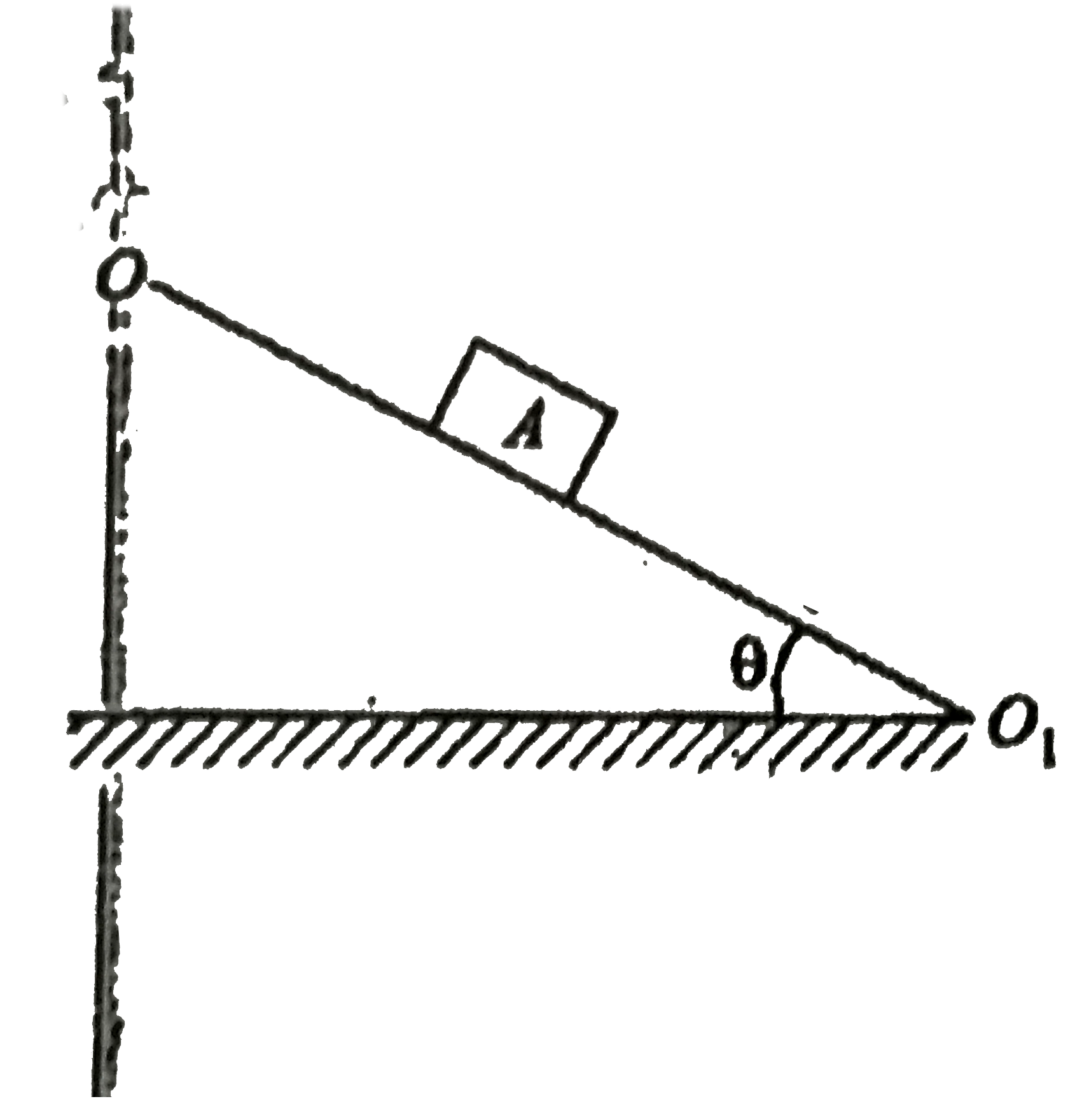 A1.5m/s2B2m/s2C2.5m/s2DNone of these
A1.5m/s2B2m/s2C2.5m/s2DNone of theseA block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
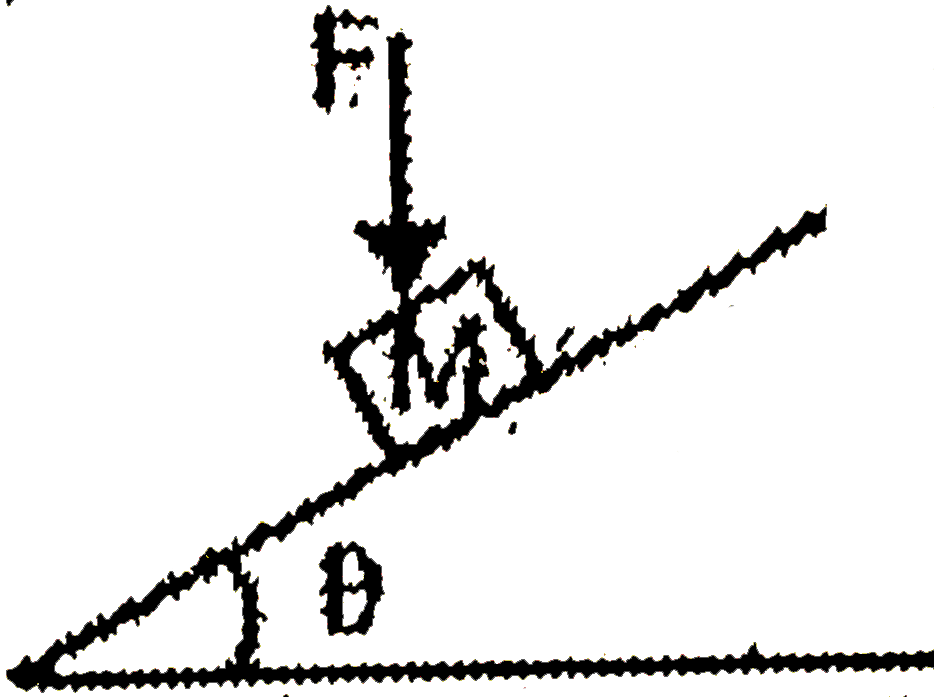 A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθ
A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθCoefficient of static friction does not depend upon
Anature and materials of the surfaces.Bnormal reactionClimiting force of static friction.Dapparent area of contact.
A block of mass m rests on a rough horizontal plane having coefficient of kinetic friction μk and coefficient of static friction μs. The spring is in its natural, when a constant force of magnitude P=5μkmg4 starts acting on the block. The spring force F is a function of extension x as F=kx2.( Where k is spring constant )

(a) Comment on the relation between μs and μk for the motion to start.
(b) Find the maximum extension in the spring ( Assume the force P is sufficient make the block move ).
View SolutionA body of mass 10 kg is kept on a horizontal floor of coefficient of static friction μs=0⋅5 and coefficient of kinetic μK=0⋅5 as shown in figure .

Find the acceleration , force of friction and contact force on the body by the plane when the driving force is (g = 10m/s2)
(i) 40 N
(ii) 60 N
View SolutionState the laws of kinetic friction. Define coefficient of kinetic friction.
View SolutionMark the correct statements about the friction between two bodies -
(a) static friction is always greater than the kinetic friction
(b) coefficient of static friction is always greater than the coefficient of kinetic friction
(c ) limiting friction is always greater than the kinetic friction
( d) limiting friction is never less than static friction
View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is

View Solution
