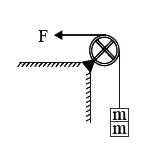
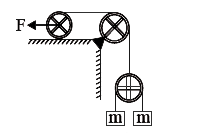
A man thinks about 4 arrangements as shown to raise two small bricks each having mass m. Which of the arrangement would take minimum time ?
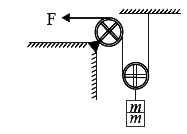

The correct Answer is:1
To solve the problem of determining which arrangement will take the minimum time to raise two small bricks each having mass m, we need to analyze the forces acting on each arrangement and how they affect the acceleration of the bricks.
1. Understanding the Arrangements:
We have four arrangements (A, B, C, D) for raising the two bricks. Each arrangement will have a different configuration affecting the forces acting on the bricks.
2. Force Analysis:
- In each arrangement, a force F is applied to lift the bricks.
- The total force acting on the bricks will determine the acceleration according to Newton's second law, F=ma.
3. Calculating Effective Force:
- For arrangement A, if both bricks are lifted directly, the effective force is 2F (since both bricks are being lifted together).
- For arrangement B, if the force is distributed, we need to analyze how much force is effectively lifting the bricks.
- For arrangement C, if there are pulleys or friction involved, we need to consider how these factors reduce the effective force.
4. Acceleration Calculation:
- The acceleration a of the bricks can be calculated using a=Feffective2m.
- The arrangement with the highest effective force will have the highest acceleration.
5. Time Calculation:
- The time taken to lift the bricks can be derived from the kinematic equation s=ut+12at2. Assuming the initial velocity u=0, we can simplify this to s=12at2.
- Rearranging gives t=√2sa. Therefore, the arrangement with the highest acceleration will take the least time.
6. Conclusion:
- After analyzing the forces and accelerations in each arrangement, we find that arrangement A, which applies the force directly to both bricks, results in the highest effective force and thus the highest acceleration.
- Therefore, Arrangement A will take the minimum time to raise the two bricks.
We have four arrangements (A, B, C, D) for raising the two bricks. Each arrangement will have a different configuration affecting the forces acting on the bricks.
- In each arrangement, a force F is applied to lift the bricks.
- The total force acting on the bricks will determine the acceleration according to Newton's second law, F=ma.
- For arrangement A, if both bricks are lifted directly, the effective force is 2F (since both bricks are being lifted together).
- For arrangement B, if the force is distributed, we need to analyze how much force is effectively lifting the bricks.
- For arrangement C, if there are pulleys or friction involved, we need to consider how these factors reduce the effective force.
- The acceleration a of the bricks can be calculated using a=Feffective2m.
- The arrangement with the highest effective force will have the highest acceleration.
- The time taken to lift the bricks can be derived from the kinematic equation s=ut+12at2. Assuming the initial velocity u=0, we can simplify this to s=12at2.
- Rearranging gives t=√2sa. Therefore, the arrangement with the highest acceleration will take the least time.
- After analyzing the forces and accelerations in each arrangement, we find that arrangement A, which applies the force directly to both bricks, results in the highest effective force and thus the highest acceleration.
- Therefore, Arrangement A will take the minimum time to raise the two bricks.
Similar Questions
Seven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is :

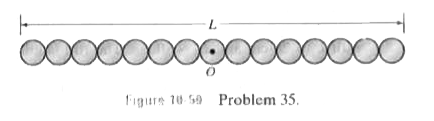
View SolutionFigure 10-59 shows an arrangement of 15 identical disks that have been glued together in a rod-like shape of length L = 1.0000 m and (total) mass M = 100.0 mg. The disks are uniform, and the disk arrangement can rotate about a perpendicular axis through its central disk at point O. (a) What is the rotational inertia of the arrangement about that axis? (b) If we approximated the arrangement as being a uniform rod of mass M and length L, what percentage error would we make in using the formula in Table 10-2e to calculate the rotational inertia?
View Solution
Knowledge Check
Two point masses, m each carrying charges −q and +q are attached to the ends of a massless rigid non - conducting wire of length L. When this arrangement is placed in a uniform electric field, then it deflects through an angle θ. The minimum time needed by the rod to align itself along the field is
A2π√mLqEBπ2√mL2qECπ√2mLqED2π√3mLqEFind the acceleration of the body of mass m2 in the arrangement shown in figure. If the massm2 is η time great as the mass m1 and the angle that the inclined plane forms with the horizontal is equal to θ. The masses of the pulley and threads, as well as the friction, are accumed to be negligible.
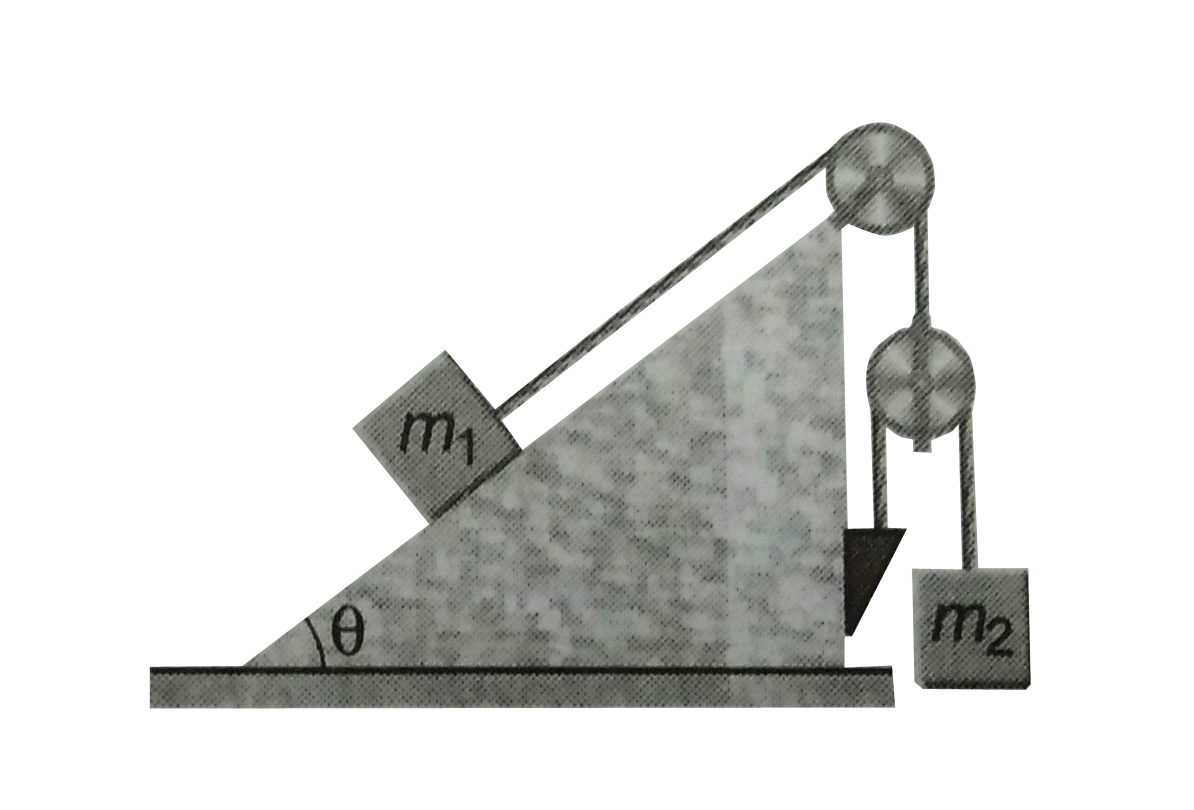 Ag(2η−sinθ)4η+1B2g(η−sinθ)4η+1C2g(2η−sinθ)η+1D2g(2η−sinθ)4η+1
Ag(2η−sinθ)4η+1B2g(η−sinθ)4η+1C2g(2η−sinθ)η+1D2g(2η−sinθ)4η+1Three rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be
 A72PQ2B27PQ2C25PQ2D52PQ2
A72PQ2B27PQ2C25PQ2D52PQ2
The arrangement shown in figure consists of two identical, uniform, solid cylinders, each of mass m, on which two light threads are wound symmetrically.
Find the tensions of each thread in the process of motion. The friction in the axle of the upper cylinder is assumed to be absent.

View SolutionIn the arrangement shown in figure, the rod of mass mhelp by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assuumming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.

View SolutionSeven homogeneous bricks, each of length L are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L10. Find the x-coordinate of the centre of mass relative to the origin shown.

View SolutionFour particles of masses m, 2m, 3m and 4m are arranged at the corners of a parallelogram with each side equal to a and one of the angle between two adjacent sides is 60∘. The parallelogram lies in the x-y plane with mass m at the origin and 4 m on the x-axis. The centre of mass of the arrangement will be located at
View SolutionFor the arrangement shown in the switch is closed at t =0. The time after which the current becomes 2.5μAS is given by (take in 2 =0.69)
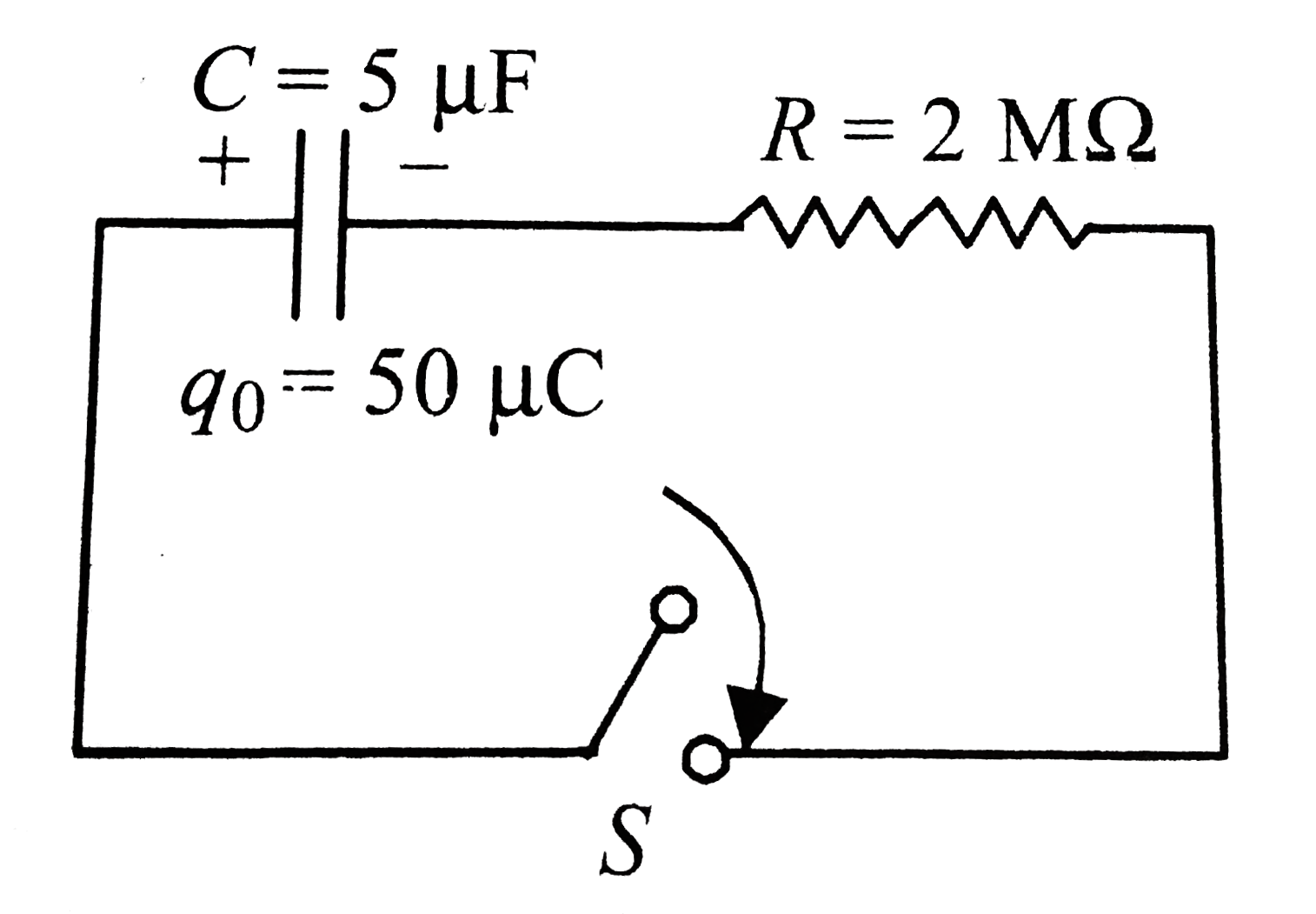
View Solution
