The three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC have the same magnitude R. Then the sum of these vectors have magnitude.
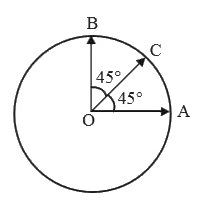
R
√2R
3R
(1+√2)R
The correct Answer is:D
Step by step video, text & image solution for The three vectors bar(OA), bar(OB) and bar(OC) have the same magnitude R. Then the sum of these vectors have magnitude. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Three vectors ¯¯¯A,¯¯¯Band¯¯¯C add up to zero. Find which is false.
View SolutionThree vectors ¯¯¯P,¯¯¯Qand¯¯¯R are shown in the figure.Let S be any point on the vector bar(R) .The distance between the points P and S is b|bar(R)| .The general relation among vectors bar(P) bar(Q) and bar(S) is qquad Y
View SolutionThree vectors bar(P) bar(Q) and bar(R) are shown in the figure.Let S be any point on the vector bar(R) .The distance between the points P and S is b|bar(R)| .The general relation among vectors bar(P) bar(Q) and bar(s) is
View SolutionIf ¯¯¯Aand ¯¯¯Bare two vectors then A new vector parallel to ¯¯¯Ahaving the magnitude of ¯¯¯Bis
View SolutionThe sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
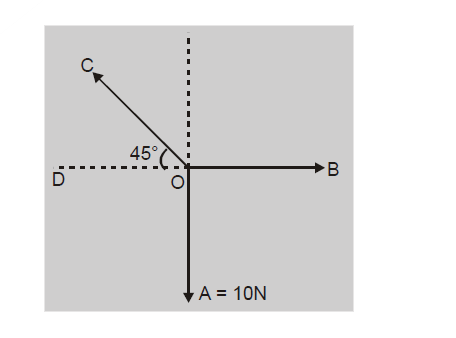
(ii) What is the magnitude of vector −−→OC ?
View SolutionAnswer the following as true or false.
(i) →aand −→aare collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude
View SolutionOABCD is a pyramid with square base ABCD such that ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB,¯¯¯¯¯¯OC,¯¯¯¯¯¯OD are unit vectors and ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB=¯¯¯¯¯¯OB.¯¯¯¯¯¯OC=¯¯¯¯¯¯OC.¯¯¯¯¯¯OD=¯¯¯¯¯¯OD.¯¯¯¯¯¯OA=12, then volume of the pyramid is
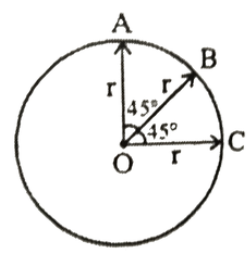
View SolutionThe resultant of the three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC shown in figure :-
View SolutionShow that the sum of the vectors represented by the sides ¯¯¯¯¯¯AB,¯¯¯¯¯¯DC of a quadrilateral ABCD as equivalent to the sum of the vectors represented by the diagonals ¯¯¯¯¯¯ACand¯¯¯¯¯¯DB.
View SolutionIf the vector −¯i+¯j−¯k bisects the angles between the vector ¯c and the vector 3¯i+4¯j ,then the unit vector in the direction of ¯c is
View Solution

