Find point B of a segment AB if A is located at (-3,7) and the midpoint of AB is located at (1,3).
(-2,10)
(-1,5)
(3,-7)
(5,-1)
The correct Answer is:D
To find point B of the segment AB given that point A is located at (-3, 7) and the midpoint of AB is located at (1, 3), we can follow these steps:
Step 1: Understand the midpoint formula
The midpoint M of a line segment AB, where A has coordinates (x1, y1) and B has coordinates (x2, y2), is given by the formula:
M=(x1+x22,y1+y22)
Step 2: Assign the known values
From the problem, we have:
- Point A: A(−3,7)
- Midpoint M: M(1,3)
- Let point B have coordinates B(x,y)
Step 3: Set up the equations using the midpoint formula
Using the midpoint formula, we can write two equations based on the coordinates of the midpoint:
1. For the x-coordinates:
1=−3+x2
2. For the y-coordinates:
3=7+y2
Step 4: Solve for x
Multiply both sides of the first equation by 2 to eliminate the fraction:
2=−3+x
Now, add 3 to both sides:
x=2+3=5
Step 5: Solve for y
Multiply both sides of the second equation by 2:
6=7+y
Now, subtract 7 from both sides:
y=6−7=−1
Step 6: State the coordinates of point B
Now we have found the coordinates of point B:
B(5,−1)
Final Answer
The coordinates of point B are (5,−1).
---
The midpoint M of a line segment AB, where A has coordinates (x1, y1) and B has coordinates (x2, y2), is given by the formula:
M=(x1+x22,y1+y22)
From the problem, we have:
- Point A: A(−3,7)
- Midpoint M: M(1,3)
- Let point B have coordinates B(x,y)
Using the midpoint formula, we can write two equations based on the coordinates of the midpoint:
1. For the x-coordinates:
1=−3+x2
2. For the y-coordinates:
3=7+y2
Multiply both sides of the first equation by 2 to eliminate the fraction:
2=−3+x
Now, add 3 to both sides:
x=2+3=5
Multiply both sides of the second equation by 2:
6=7+y
Now, subtract 7 from both sides:
y=6−7=−1
Now we have found the coordinates of point B:
B(5,−1)
The coordinates of point B are (5,−1).
Similar Questions
Knowledge Check
In the standard (x, y) coordinate plane, the midpoint of ¯¯¯¯¯¯AB is (8, -5) and B is located at (12 , -1). If (x, y) are the coordinates of A, what is the value of x + y ?
A−8B−7C−5D7Quadrilateral ABCD has point B located at (2,-1). Find the new coodinates of B once the quadrilateral is translated (4,-7)
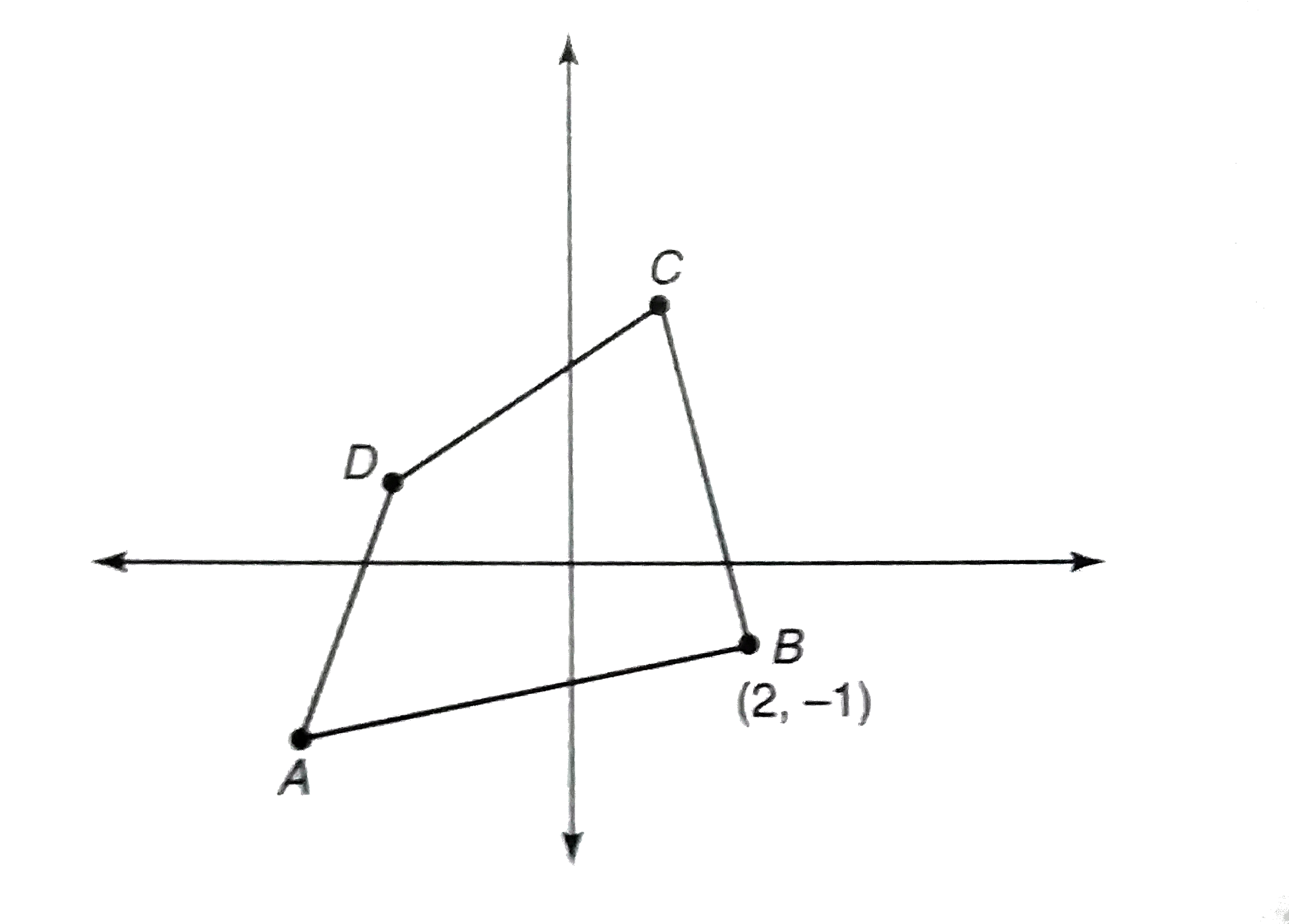 A(4,-8)B(4,-7)C(4,6)D(6,-8)
A(4,-8)B(4,-7)C(4,6)D(6,-8)Line segment ¯¯¯¯¯¯AB has midpoint (7,-1) . If point A has coordinates (2,6) , then point B has coordinates
A(92,52)B(192,−92)C(12,-8)D(14,-8)
A and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
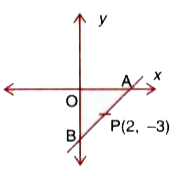
slope of line AB
View SolutionLocate the point A(3, 5, -4).
View SolutionAB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles α and β, respectively, at P, then the value of tanβ is
View SolutionP (-3, 2) is the mid point of line segment AB as shown in the given figure. Find the P (-3,2) co-ordinates of points A and B.
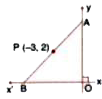
View SolutionIn the figure given below , the line segment AB meets X-axis at A and Y-axis at B. The point P (-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.
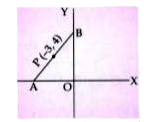
View Solution

 .
. 