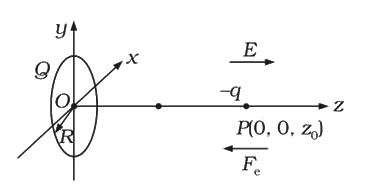
A positively charged thin metal ring of radius R is fixed in the xy plane with its centre at the origin O. A negatively charged particle P is released from rest at the point (0,0,z0) where z0>0. Then the motion of P is
periodic for all values of z0 satisfying 0<z0<∞
simple harmonic for all values of z0 satisfying 0<z0≤R
approximately simple harmonic provided z0<<R
such that P crosses O and contiude to move along the negative z-axis towards z=−∞
The correct Answer is:A, C
Let Q be the charge on the ring, the negative charge -q is released from point P(0,0,z0). The electric field at P due to the charged ring will be along positive z-axis and its magnitude will be.
E=14πε0qz0(R2+z20)3/2
E=0 at centre of the ring because z0=0. Force on charger at P will be towards centre as shown, & its magnitude is
Fe=qE=14πε0.Qq(R2+z20)3/2z0........(i)
Similarly, when it crosses the origin, the force is again towards centre O.
Thus, the motion of the particle is periodic for all values of z0 lying between 0 and ∞
Secondly, if z0<<R,(R2+z20)3/2=R3
Fe=14πε0.QqR3.z0 [From Eq. (i)]
i.e., the restoring force Feα−z0. Hence, the motion of the particle will be simple harmonic. (Here negative sign implies that the force is towards its mean position.)
Similar Questions
A circular ring of radius R with uniform positive charge density λ per unit length is located in the y z plane with its center at the origin O. A particle of mass m and positive charge q is projected from that point p(−√3R,0,0) on the negative x - axis directly toward O, with initial speed V. Find the smallest (nonzero) value of the speed such that the particle does not return to P ?
View SolutionA circular ring of radius R with uniform positive charge density λ per unit length is located in the y-z plane with its centre at the origin O. A particle of mass m and positive charge q is projected from the point P (R√3,0,0) on the positive x-axis directly towards O, with an initial speed v. Find the smallest (non-zero) value of the speed v such that the particle does not return to P.
View Solution
Knowledge Check
A positively charged ring is in y - z plane with its centre at origin . A positive test charge qe , held at origin is released along x axis, then its speed
AIncreases continuouslyBDecreases continuouslyCfirst increases then decreasesDfirst decreases then increasesA circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
Aλ3√3ε0RB2λ3√3ε0R2C23√3λε0RDnone the theseTwo equal negative charges are fixed at points and on y-axis. A positive charge Q is released from rest at the point on the x-axis. The charge Q will:
Aexecute simple harmonic motion about the originBmove to the origin and remain at restCmove to infinityDsame as at point 25 cm aways form the surface
A circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View SolutionA circular ring lying in the x-y plane with its centre at the origin carries a uniformly distributed positive charge. The variation of the electric field E at the point (0,0,z) is correctly represented by the graph is
View SolutionA circular coil with 100 turns and radius 20 cm is kept in Y-Z plane with its centre at the origin. Find the magnetic field at point (20 cm, 0, 0) if coil carries a current of2.0 A.
View SolutionA uniform semicircular ring of radius R is in yz plane with its centre at the origin. The half ring carries a uniform linear charge density of λ.
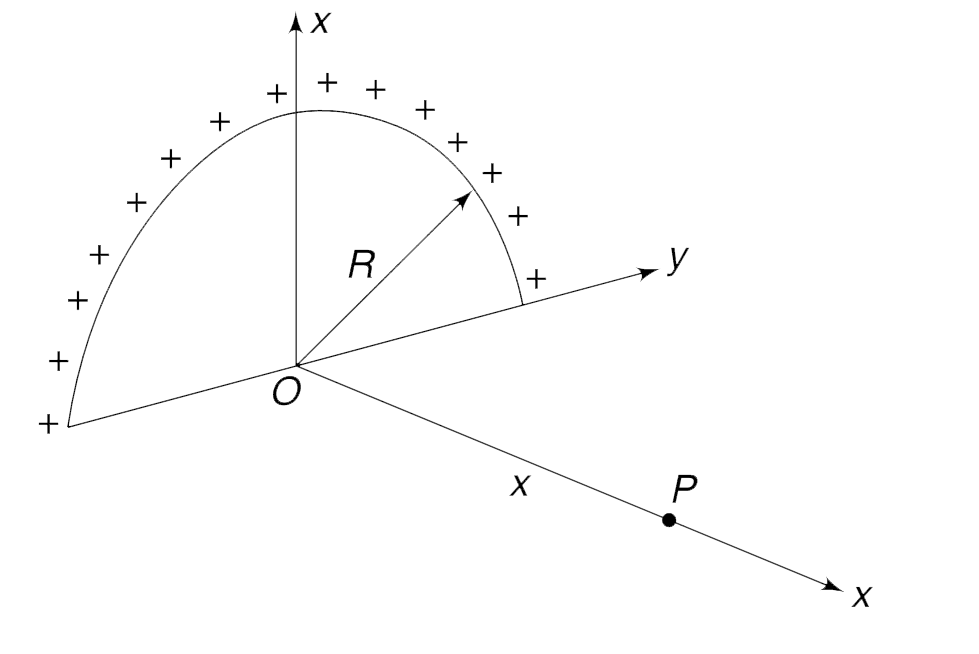
(a) Find the x, y and z component of Electric field at a point P(x, 0, 0) on the axis of the ring. (b) Prove that the field at P is directed along a line joining the centre of mass of the half ring to the point P.
View SolutionTwo equal positive charges , Q , are fixed at points (0,d) and (0,−d) on the y-axis. A charged particle having charge −q and mass m is released from rest at point (d,0) on the x-axis . Discuss the motion of charged particle.
View Solution
