A unit positive point charge of mass m is projected with a velocity v inside the tummel as shown. The tunnel has been made inside a uniformly charged non conducting sphere. The minimum velocity with which the point charge should be projected such that it can it reach the opposite end of the tunnel, is equal to:

zero because the initial and the final points are at same potential
The correct Answer is:A
If we throw the charged particle just right off the centre of the tunnel the particle will cross the tunnel. Hence applying conservation of momentum between start point and centre of tunnel we get
Or
Hence
Hence, velocity should be slightly greater than v.
Similar Questions
A point charge of charge -q and mass m is released with negligible speed from a distance √3R on the axis of a fixed uniformly charged ring of charge Q and radius R. Find out its velocity when it reaches it reaches at the centre of the ring.
 View Solution
View Solution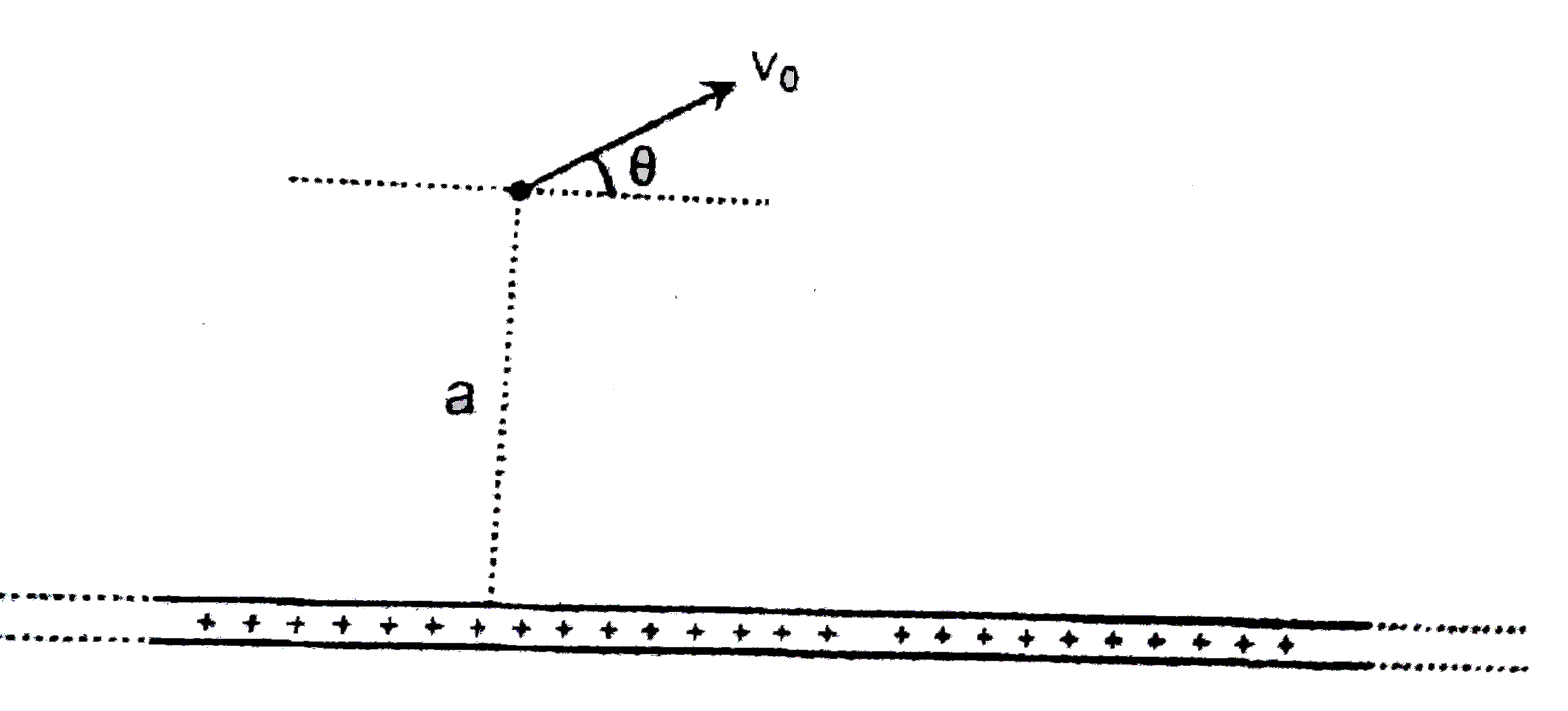
There is an infinite line of uniform linear density of charge +λ. A particle of charge −q & mass m is projected with initial velocity v0 at an angle θ with the line of charge from a distance a from it. The point charge moves in plane containing line charge and point of projection The speed of the particle of found to be minimum when it's distance from the line of charge is ae(nπmε200/qλ). The value of n is (ingnore gravity)View Solution
Knowledge Check
- Question 1 - Select One
A unit positive point charge of mass m is projected with a velocity v inside the tunnel as shown. The tunnel has been made inside a uniformly charged nonconducting sphere. The minimum velocity with which the point charge should be projected such it can it reach the opposite end of the tunnel is equal to
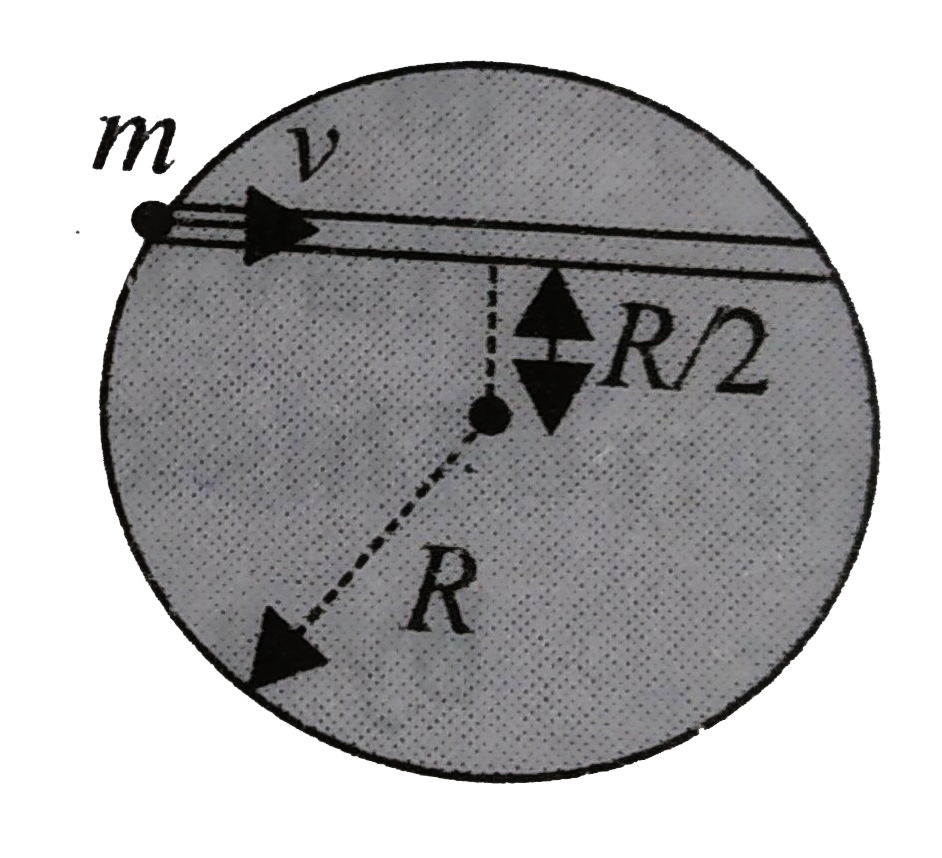 A[ρR2/4mε0]12B[ρR2/24mε0]12C[ρR2/6mε0]12Dzero because the initial and the final points are at same potential
A[ρR2/4mε0]12B[ρR2/24mε0]12C[ρR2/6mε0]12Dzero because the initial and the final points are at same potential - Question 2 - Select One
The minimum velocity v with which charge q should be projected so that it manages to reach the centre of the ring starting from the position shown in figure is
 Av=√kQqmR(2−√2)Bv=√kQq2mR(2−√2)Cv=√kQqmRDv=√kQq√2mR(1−√2)
Av=√kQqmR(2−√2)Bv=√kQq2mR(2−√2)Cv=√kQqmRDv=√kQq√2mR(1−√2) - Question 3 - Select One
The adjoining figure represent a semi-circular loop of charge Q and of radius R .The minimum velocity with which a point mass mof charge −q should be projected so that it becoems free from the influence of the loop is
 A√2Qqπε0mRB√Qqπε0mRC√Qq2πε0mRD√Qq4πε0mR
A√2Qqπε0mRB√Qqπε0mRC√Qq2πε0mRD√Qq4πε0mR
A particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.
 View Solution
View SolutionThere is a uniformly charged non-conducting solid sphere. A small spherical cavity is made inside it. Distance of the centre of cavity is x from the centre of sphere
View SolutionA charge +Q is uniformly distributed in a spherical volume of radius R. A particle of charge +q and mass m projected with velocity v0 the surface of the sherical volume to its centre inside a smooth tunnel dug across the sphere. The minimum value of v0 such tht it just reaches the centre (assume that thee is no resistance on the particle except electrostatic force) of he sphericle volume is
View SolutionThere is a uniformly charged non-conducting solid sphere. A spherical cavity is made whose centre does not coincide with the centre of solid sphere. Electric field intensity inside the cavity is
View SolutionTwo identical coaxial rings each of radius R are separated by a distance of √3R. They are uniformly charged with charges +Q and −Q respectively. The minimum kinetic energy with which a charged particle (charge +q) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is
View Solution

