A ring of radius R has charge −Q distributed uniformly over it. Calculate the charge that should be placed at the center of the ring such that the electric field becomes zero at a point on the axis of the ring at distant R from the center of the ring.
Q
Q2
Q2√2
2√2Q
The correct Answer is:C
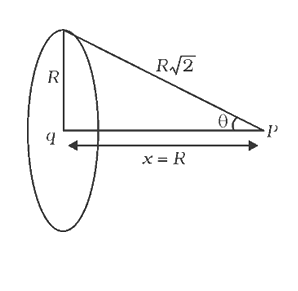
Electric field at point P due to charge of ring is E=kQx(R2+x2)3/2
At x= R, Er∈g=KQ2√2R2
Electric field at P due to center charge is Kq/R2 directed away form the center. For net field to be zero at P
KqR2=kQ2√2R2orq=Q2√2
Similar Questions
Electric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionTwo concentric rings placed in a gravity free region in yz-plane one of radius R carries a+Q and second of radius 4R and charge –8Q distributed uniformly over it. Find the velocity with which a point charge of mass m and charge +q should be projected from a a distance 3R from the centre of rings on its axis so that it will reach to the centre of the rings.
View Solution
Knowledge Check
A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field →E at the centre O is
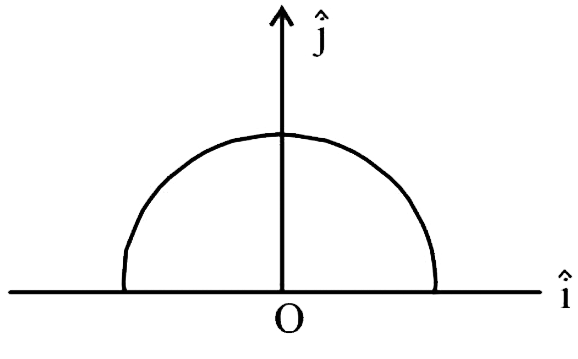 A(a) q4π2ε0r2ˆjB(b) −q4π2ε0r2ˆjC(c) −q2π2ε0r20ˆjD(d) q2π2ε0r2ˆj
A(a) q4π2ε0r2ˆjB(b) −q4π2ε0r2ˆjC(c) −q2π2ε0r20ˆjD(d) q2π2ε0r2ˆjA ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
Akq2x(a2+x2)32B2kq2x(a2+x2)32Ckq2x(a2+x2)32Dkq22x(a2+x2)32Charges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
Aq2π2ε0R2Bq4π2ε0R2Cq4πε0R2Dq2πε0R2
Over a thin ring of radius R a charge q is distributed none-uniformly. Calculate the work done of the force field in displacing a point charge q' from centre of the ring to infinity.
View SolutionA ring of radius R with a uniformly distributed charge q as shown in figure. A charge q0, is now placed at the centre of the ring. Find the increment in-the tension in ring.

View SolutionA ring of radius R is with a uniformly distributed charge Q on it .A charge q is now placed in the centre of the ring .Find the increment in tension in the ring.
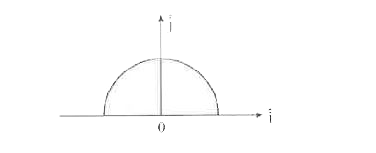
View SolutionA thin semi-circular ring of radius r has a positive charge q distributed uniformly over it as shown in the figure. The net field →E at the center O is
View SolutionA half ring of radius R has a charge of λ per unit length. The electric force on 1C charged placed at the center is
View Solution
