A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity $ω$ is an example of non=inertial frame of reference. The relationship between the force ${\to F}_{r o t}$ experienced by a particle of mass m moving on the rotating disc and the force ${\to F}_{\in}$ experienced by the particle in an inertial frame of reference is
${\to F}_{r o t} = {\to F}_{i n} + 2 m ({\to v}_{r o t} \times \to ω) + m (\to ω \times \to r) \times \to ω$ .
where ${\to v}_{r o t}$ is the velocity of the particle in the rotating frame of reference and $\to r$ is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed $ω$ about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis $(\to ω = ω ˆ k)$ . A small block of mass m is gently placed in the slot at $\to r (R / 2) ˆ i$ at $t = 0$ and is constrained to move only along the slot.

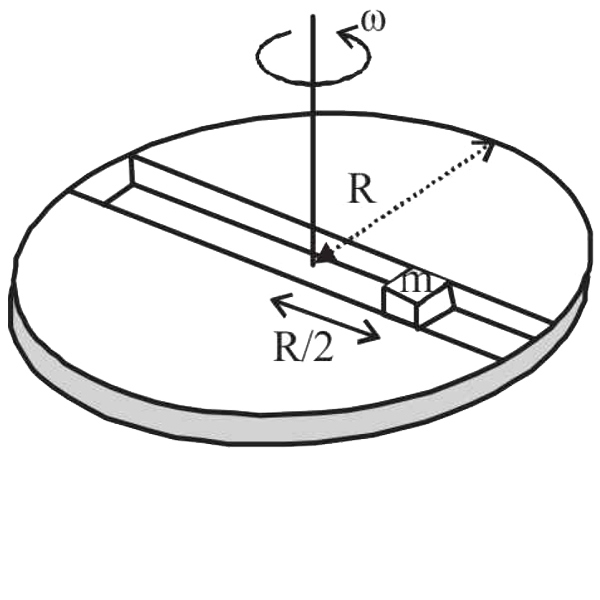
The distance r of the block at time is

$\frac{R}{2} cos 2 ω t$

$\frac{R}{2} cos ω t$

$\frac{R}{4} (e^{ω t} + e^{- ω t})$

$\frac{R}{4} (e^{2 ω t} + e^{- 2 ω t})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

In the expression ${\to F}_{e x t} = {\to F}_{\in} + 2 m (V_{r x t} \times \to ω) + m (\to ω \times \to r) \times \to ω$
The third term is radially outward i.e., this goes towards increasing ${\to V}_{r x t}$ .
2nd term is perpendicular to edge of slot and is cancelled of Normal reaction from edge of slot.
So, for radial direction.
$F = m ω^{2} r, (m d^{2} r) ({d t}^{2}) = m ω^{2} r$
i.e., $\frac{d^{2} r}{{d t}^{2}} = ω^{2} r$
Solution to this differential equation is $r = A e^{ω t} + B e^{- ω t}$
Where A and B are constants.
* for detailed solution of above differential equation see the end of this solution:
At $t = 0, r = \frac{R}{2}, \frac{R}{2} = A + B$
Also, $V_{r x t} = \frac{d r}{d t} = A ω e^{ω t} - B ω e^{- ω t}$
At t=0, $V_{r x t} = 0$ , so,
$0 = (A - B) ω, ∴ A = B - \frac{R}{4}$
So, $r = \frac{R}{4} (e^{ω t} + e^{- ω t})$
So, $r = \frac{R}{4} [e^{ω t} + e^{- ω t})]$
Hence (C) + Detailed solution of differential equation
$\Rightarrow a = ω^{2} r = v \frac{d v}{d r} \Rightarrow \int_{0}^{v} v d v = ω^{2} \int_{R / 2}^{F} r d r$
$\Rightarrow \frac{v^{2}}{2} = ω^{2} [\frac{r^{2}}{2} - \frac{R^{2}}{8}] \Rightarrow v = ω \sqrt{r^{2} - \frac{R^{2}}{4}} = \frac{d r}{d t}$
$\Rightarrow ln [\frac{r + \sqrt{x^{2} - R^{2} / 4}}{R / 2}] = ω t \Rightarrow r + \sqrt{r^{2} - R^{2} / 4} = \frac{R}{2} e^{ω t}$
$\Rightarrow r^{2} - \frac{R^{2}}{4} = {[\frac{R}{2} e^{ω t} - R]}^{2} \Rightarrow r^{2} - \frac{R^{2}}{4} = [\frac{R}{2} e^{ω t + r^{2}} - R . r e^{ω t}]$
$\Rightarrow r R e^{ω t} = R \frac{o^{2}}{4} [1 + e^{2 ω t}] \Rightarrow r = \frac{R}{4} [e^{ω t} + e^{- ω t}]$

Updated on:21/07/2023

Class 12 PHYSICS ROTATIONAL MOTION

Knowledge Check

A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity $ω$ is an example of non=inertial frame of reference. The relationship between the force ${\to F}_{r o t}$ experienced by a particle of mass m moving on the rotating disc and the force ${\to F}_{\in}$ experienced by the particle in an inertial frame of reference is
${\to F}_{r o t} = {\to F}_{i n} + 2 m ({\to v}_{r o t} \times \to ω) + m (\to ω \times \to r) \times \to ω$ .
where ${\to v}_{r o t}$ is the velocity of the particle in the rotating frame of reference and $\to r$ is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed $ω$ about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis $(\to ω = ω ˆ k)$ . A small block of mass m is gently placed in the slot at $\to r (R / 2) ˆ i$ at $t = 0$ and is constrained to move only along the slot.

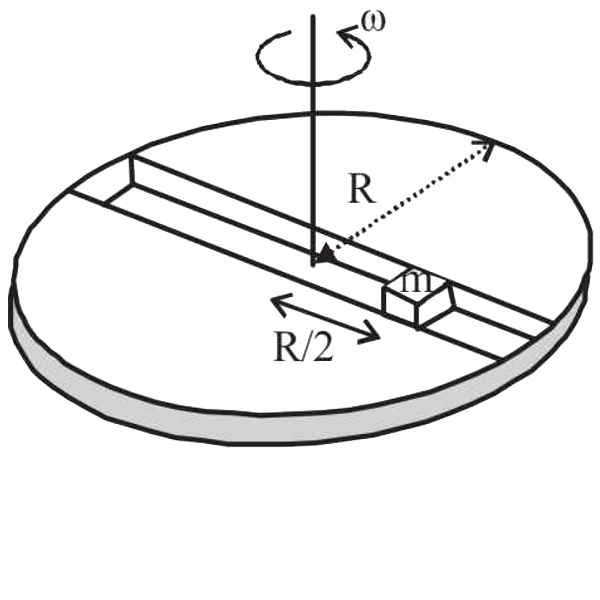
The net reaction of the disc on the block is
A(a) $\frac{1}{2} m ω^{2} R (e^{2 ω t} - e^{- 2 ω t}) ˆ j + m g ˆ k$
B(b) $\frac{1}{2} m ω^{2} R (e^{ω t} - e^{- ω t}) ˆ j + m g ˆ k$
C(c) $- m ω^{2} R cos ω t ˆ j - m g ˆ k$
D(d) $m ω^{2} R sin ω ˆ j - m g ˆ k$
Non-inertial frame of reference have
Azero acceleration.
Bsome acceleration with respect to inertial frame of reference.
Czero velocity.
Dconstant velocity with respect to inertial frame of reference.
An inertial frame of reference is, by definition,
Aa frame moving with uniform velocity w.r.t. earth
Ba frame moving with velocity w.r.t our Sun
Ca frame which is not rotating
Da frame in which Newton's first law of motion is valid.

The correct Answer is:C

Similar Questions

Knowledge Check

Non-inertial frame of reference have

An inertial frame of reference is, by definition,

Recommended Questions