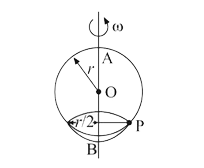
A smooth wire of length 2πr is bent into a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed about the vertical diameter AB, as shown in the figure, the bead is at rest with respect to the circular ring at potion P as shown. Then the value of ω2 is equal to:
√3g2r
2g/r
2g/(x√3)
(g√3)/r
The correct Answer is:C
Ncosθ=m(r2)ω2
Nsinθ=mg,cotθ=(rω2)

ω=2gcotθr=√2gr√3,ω2=2g√3r.
Similar Questions
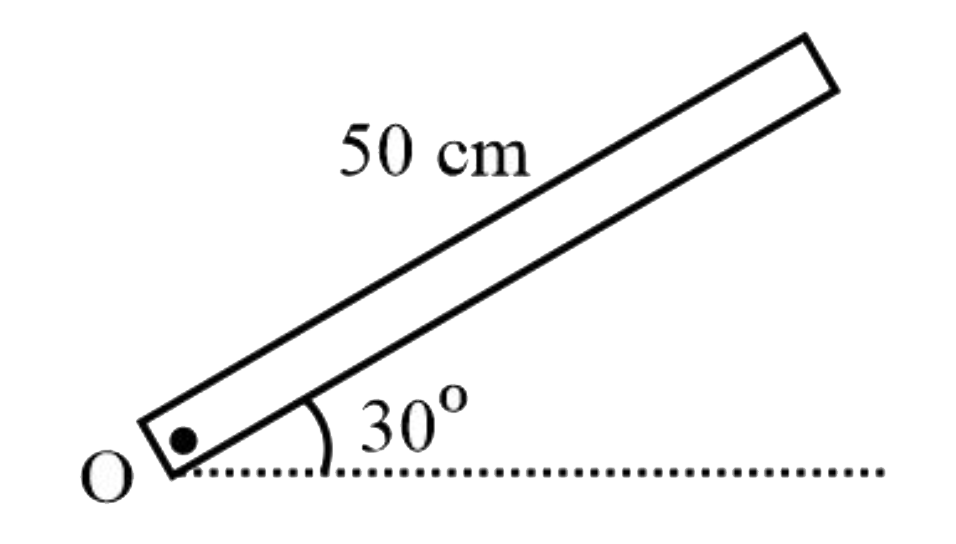
A uniform rod of length 50 cm is released in the vertical plane from the position shown in the figure. The rod is hinged smoothly at O. The angular speed of rod when it becomes horizontal is ( take g=10ms−2 )
View SolutionA wire of resistance 5Ω is bent in the form of a closed circle. Find the resistance across the diameter of the circle.
View Solution
Knowledge Check
A smooth wire is bent into a vertical circle of radius a. A bead P can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead P is at rest w.r.t. the circular ring in the position shown. then ω2 is equal to:
 A2gaB2ga√3Cg√3aD2ag√3
A2gaB2ga√3Cg√3aD2ag√3A small ring P is threaded on a smooth wire bent in the form of a circle of radius a and centre O. The wire is rotating with constant angular speed ω about a vertical diameter xy, while the ring remains at rest relative to the wire at a distance a2 from xy. Then is equal to:
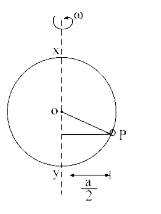 A2gaBg2aC2ga√3Dg√32a
A2gaBg2aC2ga√3Dg√32a
A small pulse is generated on a ring rotating with constant angular velocity ω as shown in the figure. Then the speed of pulse with respect to ground.AωRBωR/2C2ωRDzero
A thin circular ring of mass per unit length p and radius r is rotating at an angular speed ω as shown in figure. The tension in the ring is

View SolutionA wire of resistance 10Ω is bent to form a circle. P and Q are points on the circumference of the circle dividing it into a quadrant and are connected to a Battery of 3 V and internal resistance 1Ω as shown in the figure. The currents in the two parts of the circle are

View SolutionA piece of wire is bent in the shape of a parabola y=Kx2 (y - axis vorical) with a bead of mass m on it . The beat can side on the wire without friction , it stays the wire is now accleated parallel to the bead , where the bead can stay at rest with repect to the wire from the y - axis is
View SolutionA particle P is moving with uniform speed in a circular path . C is the centre of circle and AB is a diameter of circle. Let ωA be the angular speed is particle about C and A. Then value of ωC/ωA is
View SolutionA bead can slide on a smooth circular wire frame of radius R which is fixed in a vartical plane. The bead is displaced slightly from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the vertical line is
View Solution
