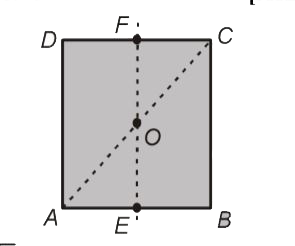
For the given uniform square lamina ABCD, whose centre is O
IAD=3IEF
IAC=IEF
IAC=√2IEF
√2IAC=IEF
The correct Answer is:B
Let the side of square be a. IEF=Ma212
By perpendicular axes theorem, the moment of inertia of lamina about an axis passing through O and perpendicular to plane of lamina I2=Ma212+Ma212=Ma26.
Again by perpendicular axes theorem, IAC+IBD=IZ⇒IAC=Iz2=Ma212
Similar Questions
For the given uniform square lamina ABCD, where centre is O. Its moment of inertia about an axis AD is equal to how many times its moment of inertia about an axis EF?
1√2IAC=IEF 2.IAD=3IEF
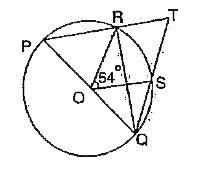
3.IAC=4IEF. 4.IAC=√2IEFView SolutionPQ is the diameter of the given circle, whose centre is O. Given, ∠Ros=54∘, calculate ∠RTS.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the adjoining diagram ABCD is a square with side 'a' cm. In the diagram the area of the larger circle with centre 'O' is equal to the sum of the areas of all the rest four circles with equal radii, whose centres are P,Q,R and S . What is the ratio between the side of square and radius of a smaller circle ?
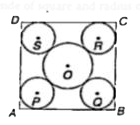 A(2√2+3)B(2+3√2)C(4+3√2)Dcan't be determined
A(2√2+3)B(2+3√2)C(4+3√2)Dcan't be determined - Question 2 - Select One
In the given figure, ABCD is a square whose side is 4 cm. P is a point on the side AD. What is the minimum value (in cm) of BP+CP?
 A4√5B4√4C6√3D4√6
A4√5B4√4C6√3D4√6
A uniform square lamina of side 10cm is hung up by a corner and swings in its won plane. Find the length of an equivalent simple pendulum.
View SolutionIn the given figure, ABCD is a square whose side is 4 cm. P is a point on the side AD. What is the minimum value (in cm) of BP+CP?
 View Solution
View SolutionIn the given figure, side of square ABCD is 7 cm. With centre D and radius DA, sector D-AXC is drawn. find out the area of the shaded ragion.
View SolutionIn the given figure, OPOR is a square. A circle drawn with centre O, cuts the square X and Y. Prove that QX=QY.
View SolutionFind the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
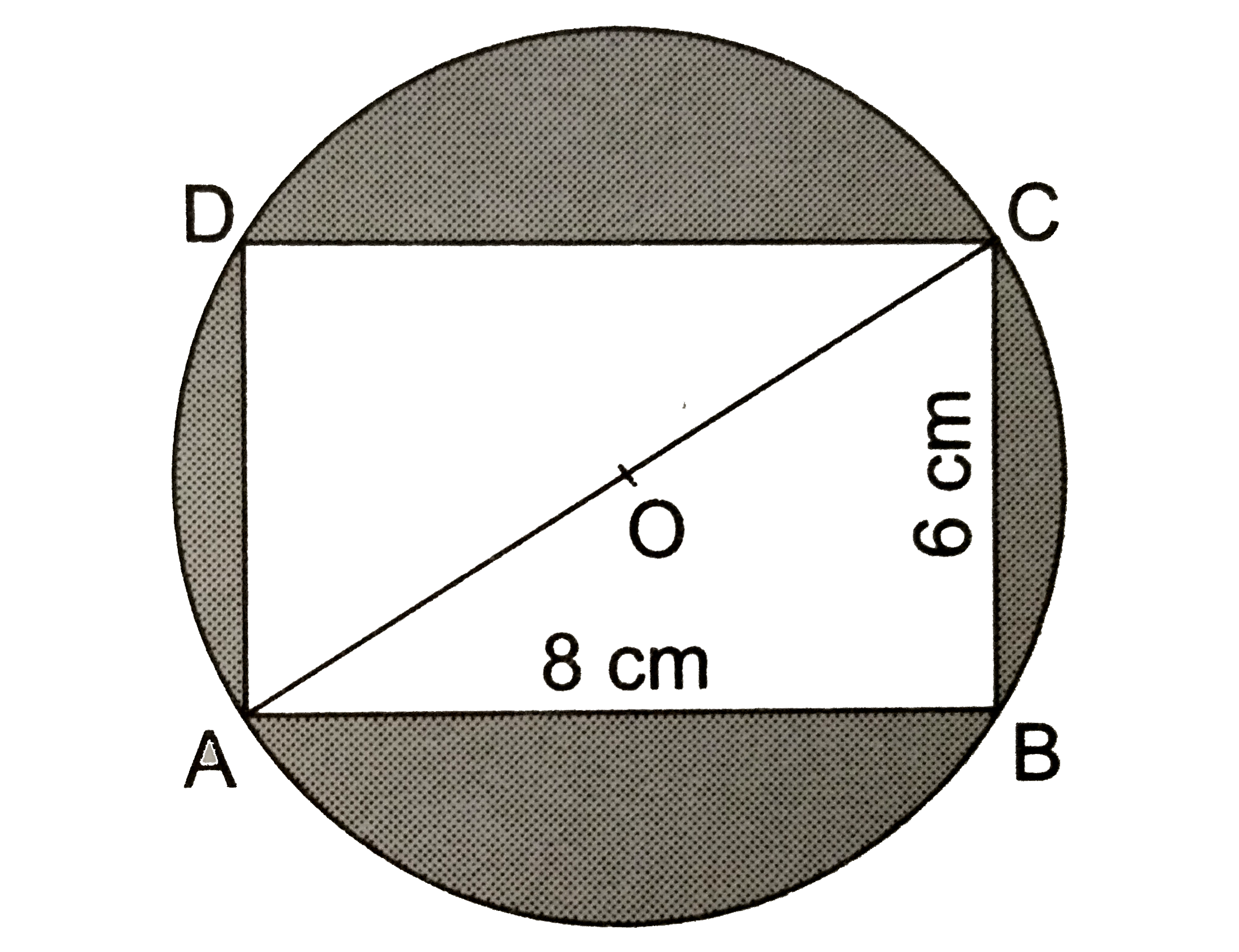 View Solution
View SolutionThere is a pentagon ABCDE, whose centre is O. Five identical charges Q are placed at the corners of pentagon.
(a)What will be the net electric field intensity at the centre of pentagon ?
(b)If charge at corner A is moved to centre O of pentagon, then what will be the net force experienced by it ?
Distance of any vertex of pentagon from its centre is d.
 View Solution
View Solution
