A wheel of radius R has an axle of radius R/5. A force F is applied tangentially to the wheel. To keep the system in a state of "rotational" rest, a force F' is applied tangentially to the axle. The value of F' is
F
3F
5F
7F
The correct Answer is:C
F'×R5=FR or F'=5F
Similar Questions
In the figure at the free end a force F is applied to keep the suspended mass of 8 kg at rest. The value of F is :
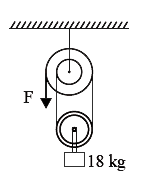
View SolutionAs shown, a wheel of weight W and radius 1.0m is placed against a 0.4m height rectangular block fixed on the ground. The wheel has an axle of radius 0.1m. A force F is applied tangentially to the axle to lift the wheel. The minimum value of F is given.by expression F=αW11. Then find the value of α.
'(##CEN_KSR_PHY_JEE_C09_E01_039_Q21##)'
View Solution
Knowledge Check
In the figure at the free end a force F is applied to keep the suspended mass of 18 kg at rest. The value of F is-
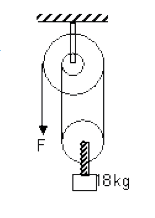 A180 NB90 NC60 ND30 N
A180 NB90 NC60 ND30 NA whel of mass 2kg an radius 10 cm is rotating about its axis at an angular velocity of 2πrad/s the force that must be applied tangentially to the wheel to stop it in 5 revolutions is
A3π×10−2kg−m2/sB4π×10−2kg−m2/sCπ×10−2kg−m2/sD2π×10−2kg−m2/sA wheel of radius R, mass m with an axle of radius r is placed on a horizontal surface. Its moment of inertia is I=mR2. Unwinding a rope from its axel a force F is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling (∠θ=0∘)

Find the linear acceleration of the wheelAF[I/m−Rr][(I/m)+r2]B2F[(I/m)−Rr][(1/m)+r2]CF[(2I/m)−√2Rr][(I/m)+r2]DF[(I√2/m)−Rr][(I/m)+r2]
A wheel of mass 10 kg and radius 0.2 m is rotating at an angular speed of 100 rpm, when the motion is turned off. Neglecting the friction at the axis. Calculate the force that must be applied tangentially to the wheel to bring it to rest in 10 rev. Assumed wheel to be a disc.
View SolutionA wheel of mass 10 kg and radius 0.2 m is rotating at an angular speed of 100 rpm, when the motion is turned off. Neglecting the friction at the axis. Calculate the force that must be applied tangentially to the wheel to bring it to rest in 10 rev. Assumed wheel to be a disc.
View SolutionA wheel of radius R, mass m with an axle of radius r is placed on a horizontal surface. Its moment of inertia is I=mR2. Unwinding a rope from its axel a force F is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling (∠θ=0∘)

Find the condition for which frictional force acts in backward direction
View SolutionA wheel of radius R, mass m with an axle of radius r is placed on a horizontal surface. Its moment of inertia is I=mR2. Unwinding a rope from its axel a force F is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling (∠θ=0∘)

Find the condition for which frictional force acts in forward direction
View SolutionA wheel of radius R with an axle of radius R/2 is shown in the figure and is free to rotate about a frictionless axis through its centre and perpendicular to the page. Three forces (F, F, 2F) are exerted tangentially to the repective rims as shown in the figure.
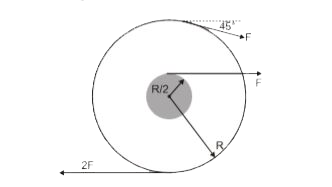
The magnitude of the net torque acting on the system is nearly
View Solution
