The angular momentum of a particle about origin is varying as L =4t+8(SI units) whern its moves along a straight line y=x-4(x,y in metres). The magnitude of force acting on the particle will be
The correct Answer is:1.41
L=4t + 8
Torque about the origin, τ=dLdt=4N−m,
τ=r1F,4=r1F, where, r1 is the perpendicular distance of origin from a line:
r1=∣∣
∣∣0−0−4√12+12∣∣
∣∣=2√2
Force is acting along the straight line
x−y−4=0, F=√2N=1.41N.
Similar Questions
A particle of mass 80 units is moving with a uniform speed v=4√2 units in XY plane, along a line y=x+5. The magnitude of the angular momentum of the particle about the origin is
View SolutionA particle of mass 1kg is moving alogn the line y=x+2 with speed 2m/sec. The magnitude of angular momentum of the particle about the origin is
View Solution
Knowledge Check
Kinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
ADirectly proportional to the speed of the particleBInversely proportional to √tCInversely proportional to the speed of the particleDDirectly proportional to √tKinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
Ais constantBis increasingCis decreasingDfirst increase and then decreasesThe kinetic energy K of a particle moving along x axis varies with its position (x) as shown in the figure. The magnitude of force acting on particle at x = 9 m is -
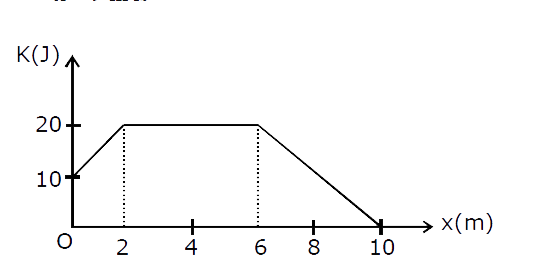 AzeroB5 NC20 ND7.5 N
AzeroB5 NC20 ND7.5 N
The kinetic energy K of a particle moving along x - axis varies with its position (x) as shown in figure

The magnitude of force acting on particle at x = 9 mis
View SolutionA particle of mass m=5 unit is moving with a uniform speed v=3√2 unit in the XOY plane along the line y=x+4 the magnitude of the angular momentum of the particle about the origin is
View SolutionA particle of mass m=5 unit is moving with a uniform speed v=3√2 unit in the XOY plane along the line y=x+4 the magnitude of the angular momentum of the particle about the origin is
View SolutionA particle of mass m=5kg is moving with a uniform speed v=3√2 in the XOY plane along the line Y=X+4. The magnitude of the angular momentum of the particle about the origin is
View SolutionThe kinetic energy K of a particle moving along x - axis varies its position (x) as shown in figure.

The magnitude of force acting on particle at x = 9m is
View Solution
