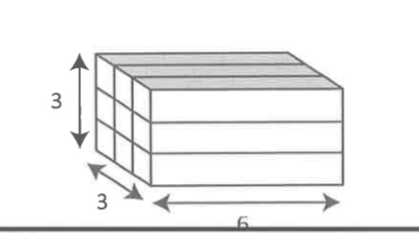
The large rectangular solid shown here is formed by binding together nine identical rectangular rods, as shown.
Quantity AQuantity BFour times the surface are ofThe surface area of the largejust one of the identicalrectangular solid aboverectangular rods
The correct Answer is:Quantity A is greater.
Step by step video, text & image solution for The large rectangular solid shown here is formed by binding together nine identical rectangular rods, as shown. {:("Quantity A","Quantity B"),("Four times the surface are of","The surface area of the large"),("just one of the identical","rectangular solid above"),("rectangular rods",):} by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
The figure here shows two wooden cubes joined to form a rectangular solid. If each cube has a surface are of 24, what is the surface are of the resulting rectangular solid?View SolutionA rectangular solid has square base, with each side of the base measuring 4 meters. If the volume of the solid is 112 cubic meters, what is the surface area of the solid?
View Solution
Knowledge Check
- Question 1 - Select One
The surface area of a rectangular solid measuring 5×6×8 is how much greater than the surface area of a rectangular solid measuring 3×6×8?
A12B24C48D56
A rectangular strip 25cm x 7cm is rotated about the longer side. Find the total surface area of the solid thus generated.
View SolutionA rectangular strip 25cm x 7cm is rotated about the longer side. Find the total surface area of the solid thus generated.
View SolutionThe given quantity of metal is to be cost into a half cylinder with a rectangular base and semicircular ends. Show that in order that the total surface area may be minimum, the ratio of the length of the cylinder to the diameter of its semi-circular ends is π:(π+2).
View SolutionThe given quantity of metal is to be cost into a half cylinder with a rectangular base and semicircular ends. Show that in order that the total surface area may be minimum, the ratio of the length of the cylinder to the diameter of its semi-circular ends is π:(π+2).
View SolutionThe length, breadth and height of a rectangular solid are in the ratio 5:4,2. If the total surface area is 1216cm2, find the length, the breadth and the height of the solid.
View SolutionFrom a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find :
the surface area of remaining solid,View SolutionA given quantity of metal is to be cast into a half cylinder with a rectangular base and semicircular ends. Show that in order for the total surface area to be minimum, the ratio of the length of the cylinder to the diameter of its semi-circular ends is π:(π+2).
View Solution

