What is the sum of the interior angles of an octagon (eight - sided polygon)?
The correct Answer is:1,080∘
Step by step video, text & image solution for What is the sum of the interior angles of an octagon (eight - sided polygon)? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
We know that the sum of the interior angles of a triangle is1800 . Show that the sums of eth interior angles of polygons with 3,4,5,6, sides for an arithmetic progression. Find the sum of the interior angles of or a 21 sided polygon.
View SolutionWe know that the sum of the interior angles of a triangle is1800 . Show that the sums of the interior angles of polygons with 3,4,5,6 sides form an arithmetic progression. Find the sum of the interior angles of a 21 sided polygon.
View Solution
Knowledge Check
The measure of the sum of the interior angles of a regular n-sided polygon is (n-2)180∘. A regular octagon is shown below. What is the measure of the designated angle ?
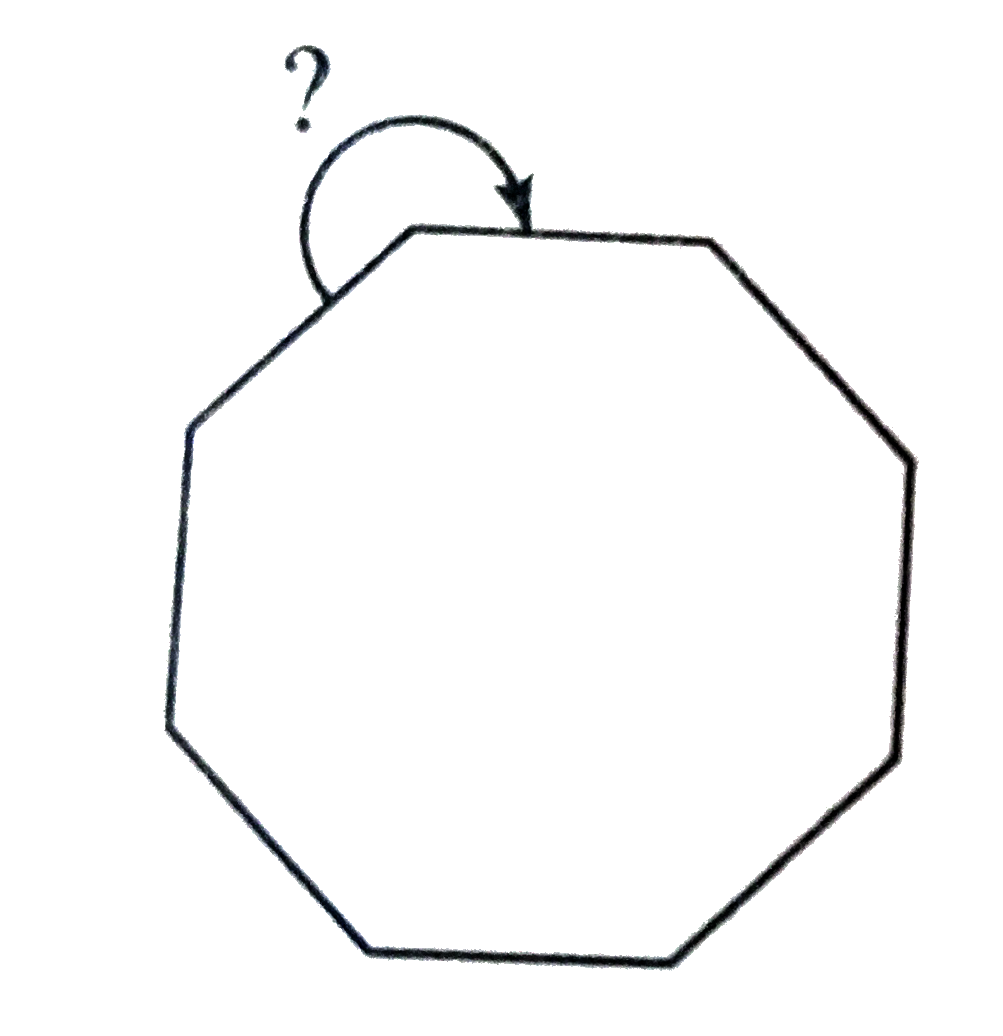 A135∘B144∘C200∘D225∘
A135∘B144∘C200∘D225∘The sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.
A8B7C5D9
A regular polygon in which every side is of equal length and all interior angles are equal. What is the degree measur of each interior angle in a regular hexagon (six - sided polygon)?
View SolutionThe sum of the interior angles of a regular polygon is equal to six times the sum of exterior angles. Find the number of sides of the polygon.
View SolutionThe sum of the interior angles of a polygon is four times the sum of its exterior angles. Find the number of sides in the polygon.
View SolutionThe sum of the interior angles of a polygon is five times the sum of its exterior angles. Find the number of sides in the polygon.
View SolutionThe sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.
View SolutionThe number of diagonals of a regular polygon is 27. Then, find the measure of each of the interior angles of the polygon.
View Solution
