particles of masses 2M m and M are resectively at points A , B and C with AB=12(BC) m is much - much smaller than M and at time t=0 they are all at rest as given in figure . As subsequent times before any collision takes palce .
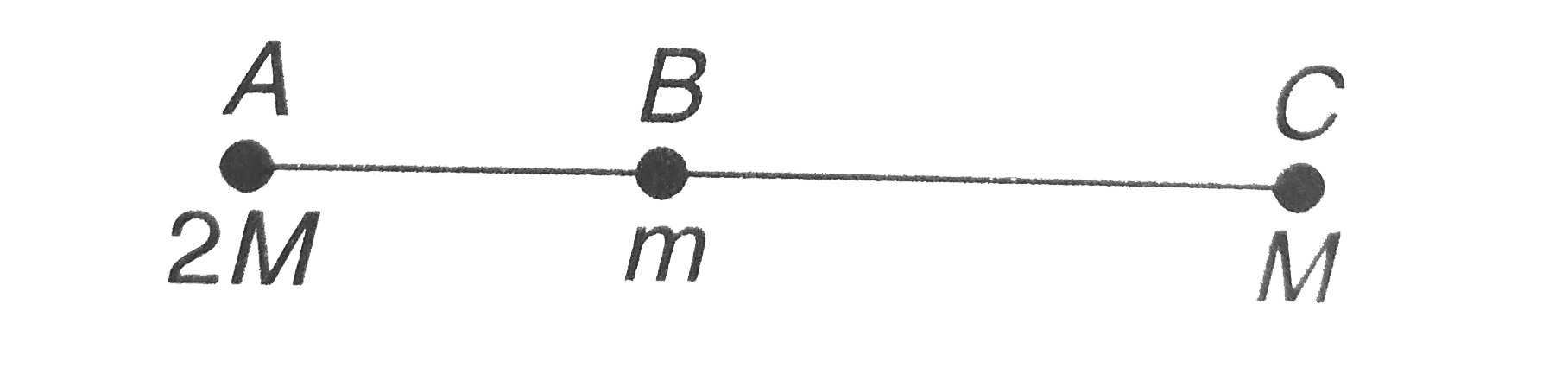
m will remain at rest
m will move towards M
m will move towards 2M
m will have oscillatory motion
The correct Answer is:C
Force on B due to A=FBA=G(2Mm)(AB)2 towards BA
Force on B due to C=FBC=GMm(BC)2 towards BC
As, (BC)=2AB
⇒FBC=GMm(2AB)2=GMm4(AB)2≤FBA
Hence, m will move towards BA (i.e., 2M)
Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT EXEMPLARCHAPTER - GRAVITATIONEXERCISE - Very short Answer type question
11 Videos
- GRAVITATIONBOOK - NCERT EXEMPLARCHAPTER - GRAVITATIONEXERCISE - Short Answer type question
6 Videos
- KINETIC THEORYBOOK - NCERT EXEMPLARCHAPTER - KINETIC THEORYEXERCISE - Multiple Choice Questions (MCQs)
31 Videos
Similar Questions
consider a head on collision between two particles of masses m1andm2. The initial speeds of the particles are u1andu2 in the same directioin. The collision starts at t=0 and the particles interact for a time inteval △t. Lduring the collision the speed o the first particle varies as
v(t)=u1+t/v1−u1 Find the speed of the second particle as as function of time during the collision.
View SolutionA particle of mass m is released from rest and follows a particle as a function of time?
View Solution
Knowledge Check
Particles of masses 2M, m and M are respectively at points A, B and C with √GMR(√2+1) is much-much smaller than M and at time t=0, they are all at rest as given in figure
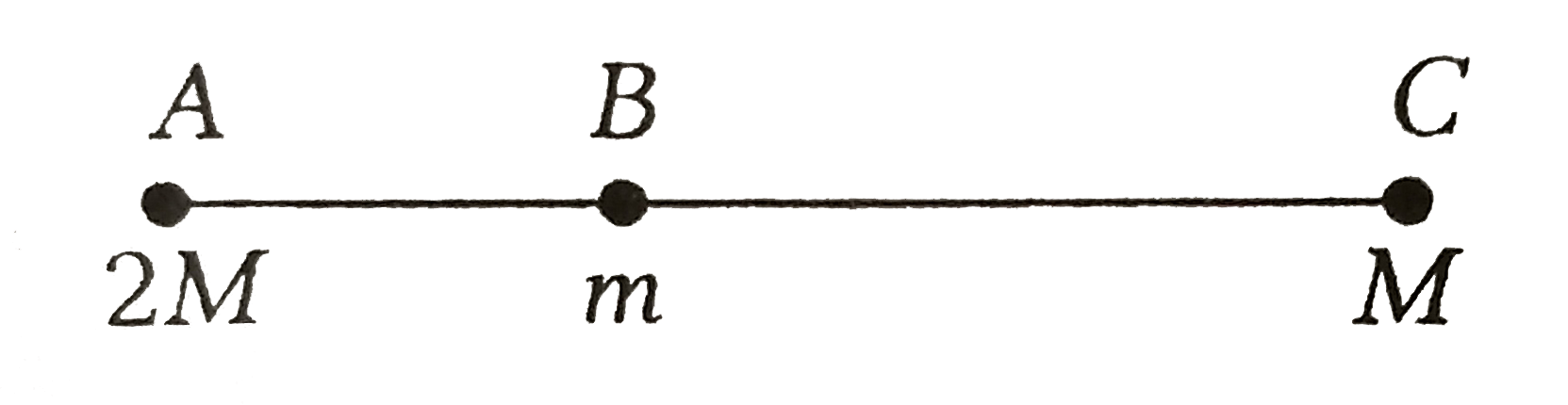
At subsequent time before any collision takes place.Am will remain at restBm will move towards MCm will move towards 2MDm will have oscillatory motionTwo particle of masses m and 2m are coliding elastically as given in figure. If V1 and V2 speed of particle just after collision then
_2019_CBT5_E01_051_Q01.png)
AV1=11.16m/s,V2=6.31m/sBV1=10.16m/s,V2=5.31m/sCv1=9.16M/S,v2=6.31M/SDv1=6.31M/S,v2=11.16M/SA particle A of mass m initially at rest slides down a height of 1.25 m on a frictionless ramp, collides with and sticks to an identical particles B of mass m at rest as shown in the figure.
Then, particles A and B together collide elastically with particle G of mass 2m at rest. The speed of particle G after the collision with combined body (A+B) would be (Take, g=10ms−2)A2ms−1B1.25ms−1C2.5ms−1D5ms−1
Blocks of masses m , 2m , 4m and 8m are arranged in a line on a frictionless floor . Another block of mass m , moving with speed v along the same line (see figure ) collides with mass m in perfectly inelastic manner. All the subsequent collisions are also perfectly inelastic. By the time the last block of mass 8 m starts moving the total energy loss is p% of the original energy . Value of 'p' is close to :
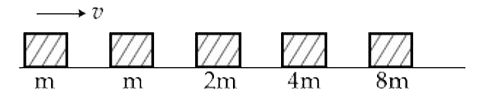
View SolutionTwo particles of masses m1andm2 in projectile motion have velocities →v1and→v2 respectively at time t=0. They collide at time t0. Their velocities become →v1'and→v2' at time 2t0 while still moving in air. The value of |(m1→v1'+m2→v2')−(m1→v1+m2→v2)| is
View SolutionA particle of mass m collides elastically with the pan of mass (M = 2m) of a spring balance, as shown in figure. Pan is in equillibrium before collision. Spring constant is k and speed of the particle before collision is v0 . Answer the following three questions regarding this collision.
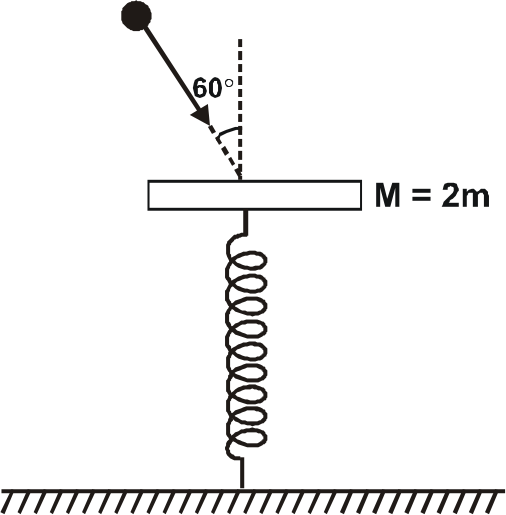
Minimum kinetic energy of the particle after collision is
View SolutionAt time t=0, a particle is at (−1m,2m) and at t=2s it is at (−4m,6m). From this we can conclude that in the given time interval.
View SolutionA particle of mass m collides elastically with the pan of mass (M = 2m) of a spring balance, as shown in figure. Pan is in equillibrium before collision. Spring constant is k and speed of the particle before collision is v0 . Answer the following three questions regarding this collision.
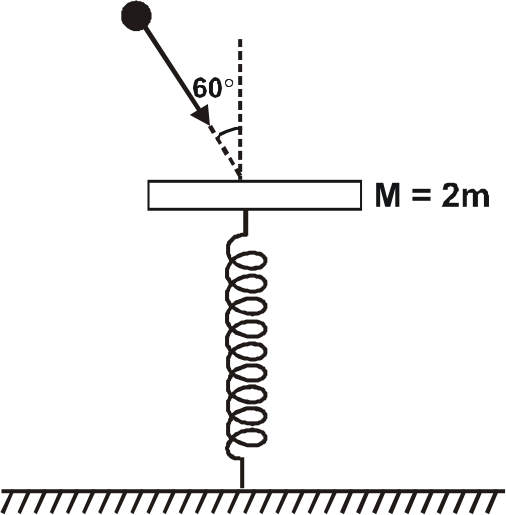
Maximum compression in the spring after the collision the
View Solution