X and Y are two volatile liquids with molar weights of 10gmol−1 and 40gmol−1 respectively. Two cotton plugs, one soaked in X and the other soaked in Y, are simultaneously placed at the ends of a tube of length L=24 cm, as shown in the figure.
The tube is filled with an inert gas at 1 atm pressure and a temperature of 300K. Vapours of X and Y react to form a product whichh is first observed at a distance dcm from the plug soaked in X.
Take X and Y to have equal molecular diameters and assume ideal behaviour for the inert gas and two vapours.
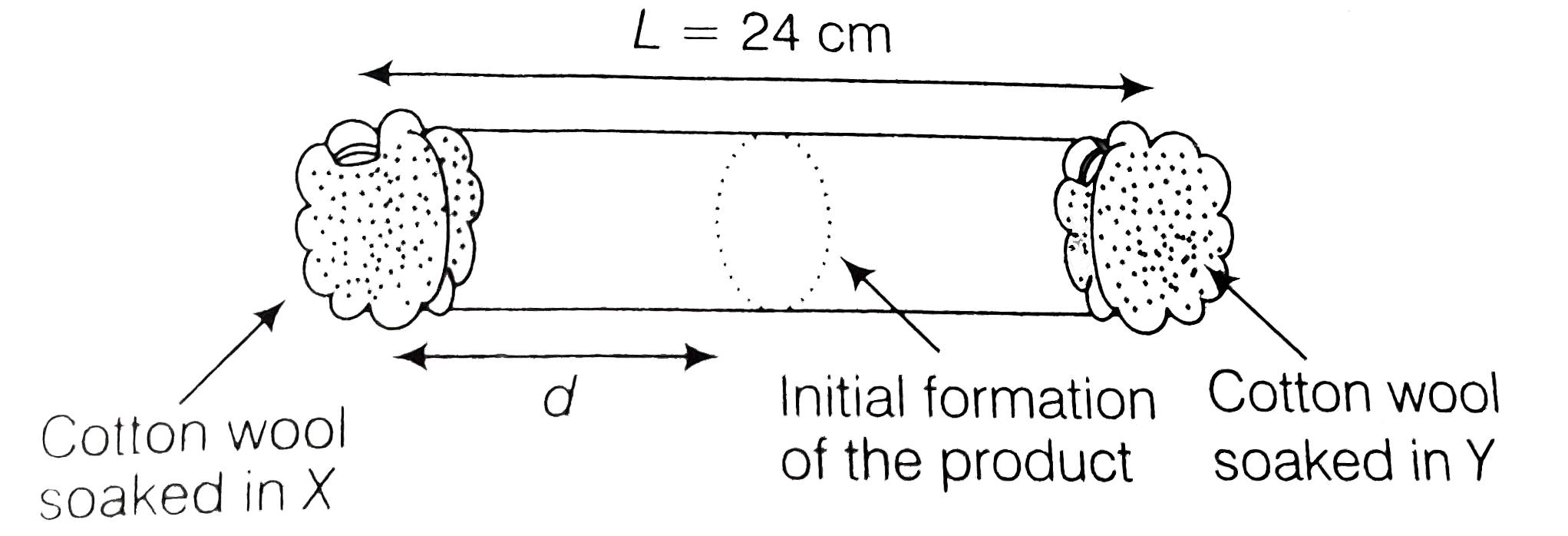
The value of d in cm (shown in figure), as estimated from Graham's law, is
8
12
16
20
The correct Answer is:C
PLAN: This problem can be solved by using the concept of Graham’s law of diffusion according to which rate of diffusion of non-reactive gases under similar conditions of temperature and pressure are inversely proportional to square root of their density.
Rate of diffision ∝1√molar weight of gas
Let distance covered by X is d, then distance covered by Y is 24-d.
If rXandry are the rate of diffusion of gases X and Y,
rxry=d24−d=√4010=2 [ ∵ Rate of diffusion distance travelled]
d=48−2d⇒3d−48⇒d=16cm
Similar Questions
A tube of length 50 cm is containing a gas in two secitons separated by a mercury column of length 10cm as shown in figure. The tube's open end is just inside the Hg surface in container, find pressure of gas in upper section. [Assume atmospheric pressure = 75 cm of Hg column]

View SolutionTwo liquids X and Y boil at 110∘C and 130∘C, respectively. Which one of them has higher vapour pressure at 50∘C?
View Solution
Knowledge Check
X and Y are two volatile liquids with molar weights of 10gmol−1 and 40gmol−1 respectively. Two cotton plugs, one soaked in X and the other soaked in Y, are simultaneously placed at the ends of a tube of length L=24 cm, as shown in the figure.
The tube is filled with an inert gas at 1 atm pressure and a temperature of 300K. Vapours of X and Y react to form a product whichh is first observed at a distance dcm from the plug soaked in X.
Take X and Y to have equal molecular diameters and assume ideal behaviour for the inert gas and two vapours.
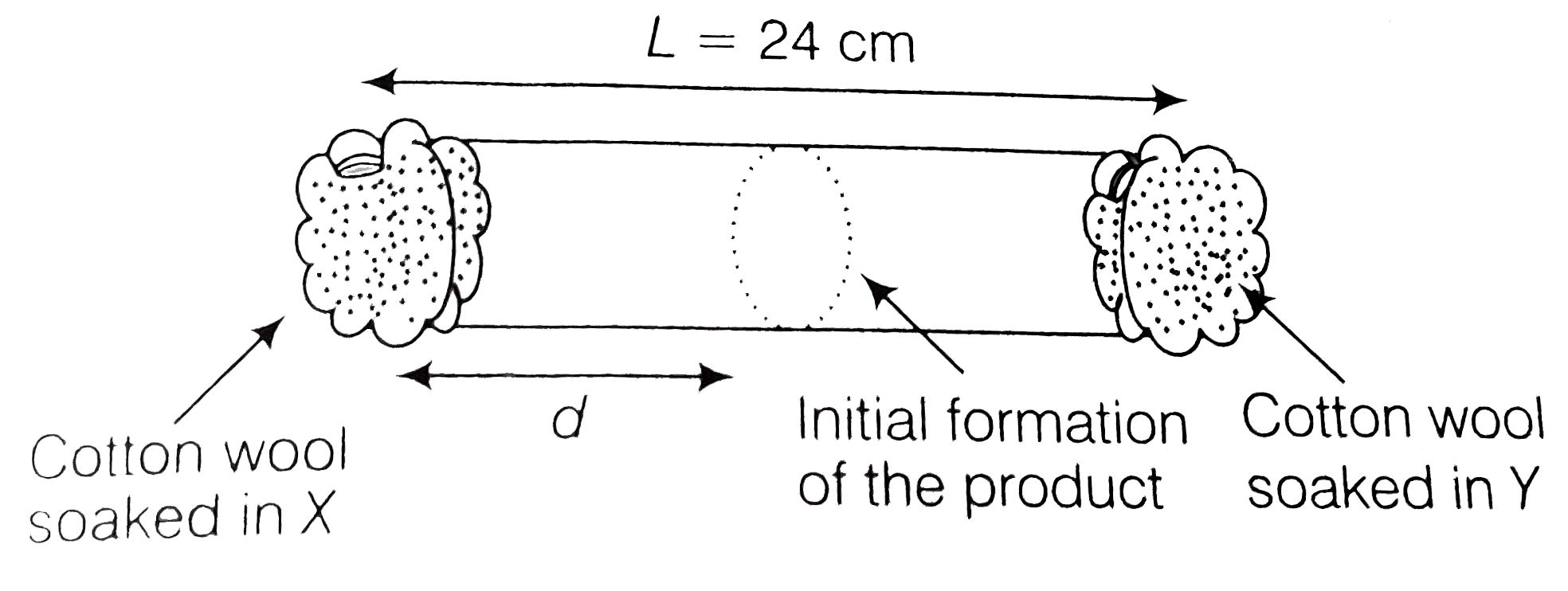
The experimental value of d is found to be smaller than the estimate obtained using Graham's law. This is due toAlarger mena free path for X as a compared of that of YBlarger mean free path for Y as compared to that of XCincreased collision frequency of Y with the inert gas as compared to that of X with the inert gasDincreased collision frequency of X with the inert gas as compared to that of Y with the inert gasTwo pieces of cotton wool soaked separetely in aqueous solution of NH3 and HCl are placed at opposite ends of a close glass tube as shown in diagram
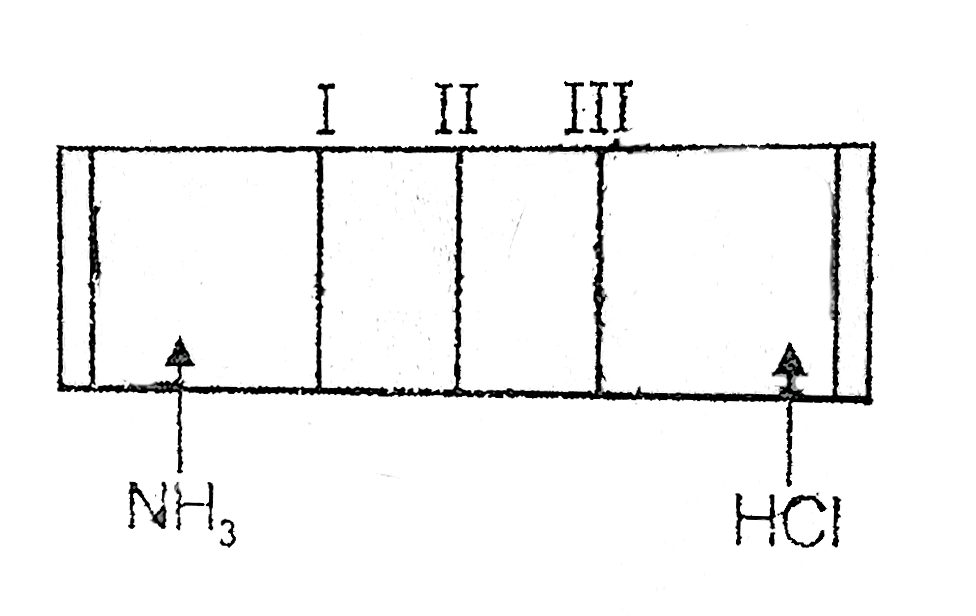
Select nearest position where white solid is formedAIBIICIIIDWhite solid does not formed
Two liquids which do not react chemically are placed in a bent tube as shown in figure. The height of the liquids above their surface of separation areAdirectly proportional to their densitiesBinversely proportional to their densitiesCdirectly proportional to square of their densitiesDinversely proportional to square of theire densities.
In two containers X and Y same gas is filled. If the pressure, volume and absolute temperature of gas in X are three times as compared to that in Y and if the mass of X is mg, the mass of Y is
View SolutionEqual weights of two gases of molecular weight 4 and 40 are mixed. The pressure of the mixture is 1.1 atm. The partial pressure of the light gas in this mixture is
View SolutionEqual weights of two gases of molecular weight 4 and 40 are mixed. The pressure of the mixture is 1.1 atm. The partial pressure of the light gas in this mixture is
View SolutionA liquid of density ρ is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h1andh2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is
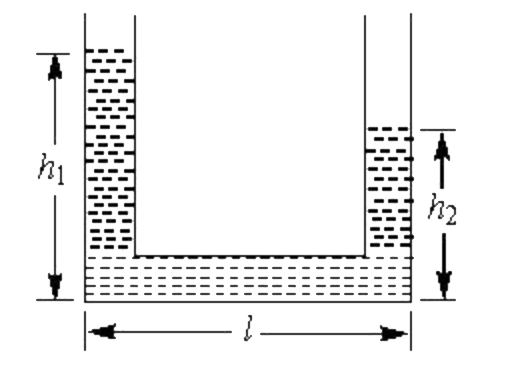
View SolutionIn the given figure, atmospheric pressure p0=1 atm and mercury column length is 9 cm. Pressure p of the gas enclosed in the tube is

View Solution
