A wire carrying current I is tied between points P and Q and is in the shape of a circular arc of radius R due to a uniform magnetic field B (perpendicular to the plane of the paper, shown by xxx) in the vicinity of the wire. If the wire subtends an angle 2θ0 at the centre of the circle (of which it forms an arc) then the tension in the wire is:

IBR
IBRsinθ0
IBR2sinθ0
IBRθ0sinθ0
The correct Answer is:A
Magnetic force on the circular arc
F=I(2Rsinθ0)B
for the arc to be in equilibrium F=2Tsinθ0
∴2Tsinθ0=2IRsinθ0B,T=IRB

Similar Questions
A piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionIf the piece of wire 25 cm long is bent into an arc of a circle subtending an angle of 75∘ at the centre , then the radius of the circle ( in cm ) is :
View Solution
Knowledge Check
A wire carrying current I is tied between points P and Q and is in the shape of a circular arch of radius R due to a uniform magnetic field B (perpendicular to the plane of the paper, shown by cross marked) in the vicinity of the wire. If the wire subtends and angle 2θ0 at the centre of the circle of which it forms an arch) then the tension in the wire is:
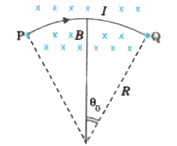 AIBRBIBRsinθ0CIBR2sinθ0DIBRθ0sinθ0
AIBRBIBRsinθ0CIBR2sinθ0DIBRθ0sinθ0A current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
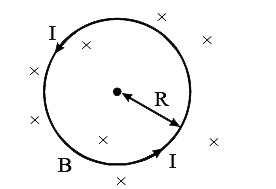 ABIRB2πBIRCπBIRD2BIR
ABIRB2πBIRCπBIRD2BIRA straight wire carrying a current 10A is bent into a semicircular arc of radius 5cm. The magnitude of magnetic field at the center is
A1.5×10−5TB3.14×10−5TC6.28×10−5TD19.6×10−5T
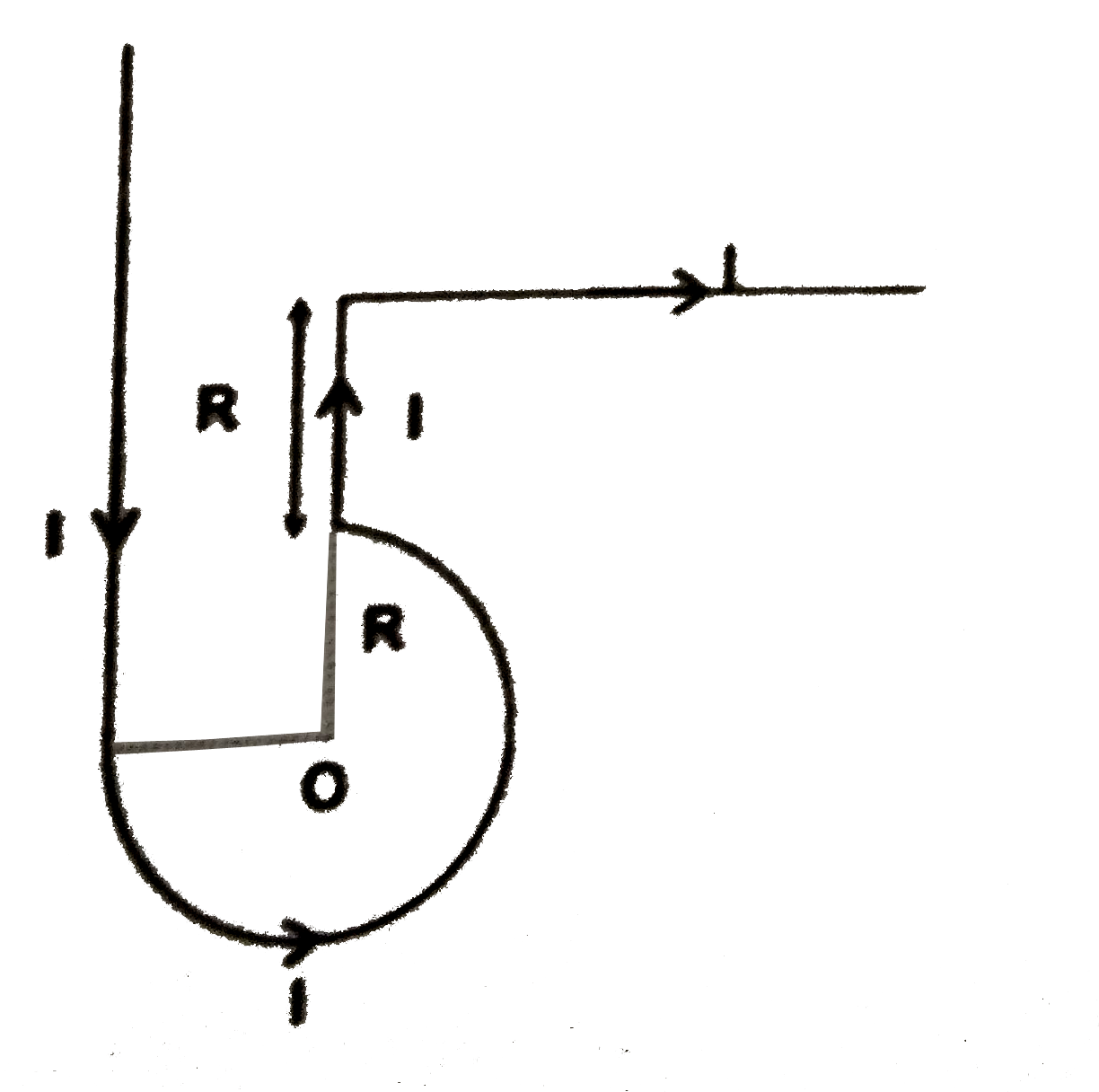
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
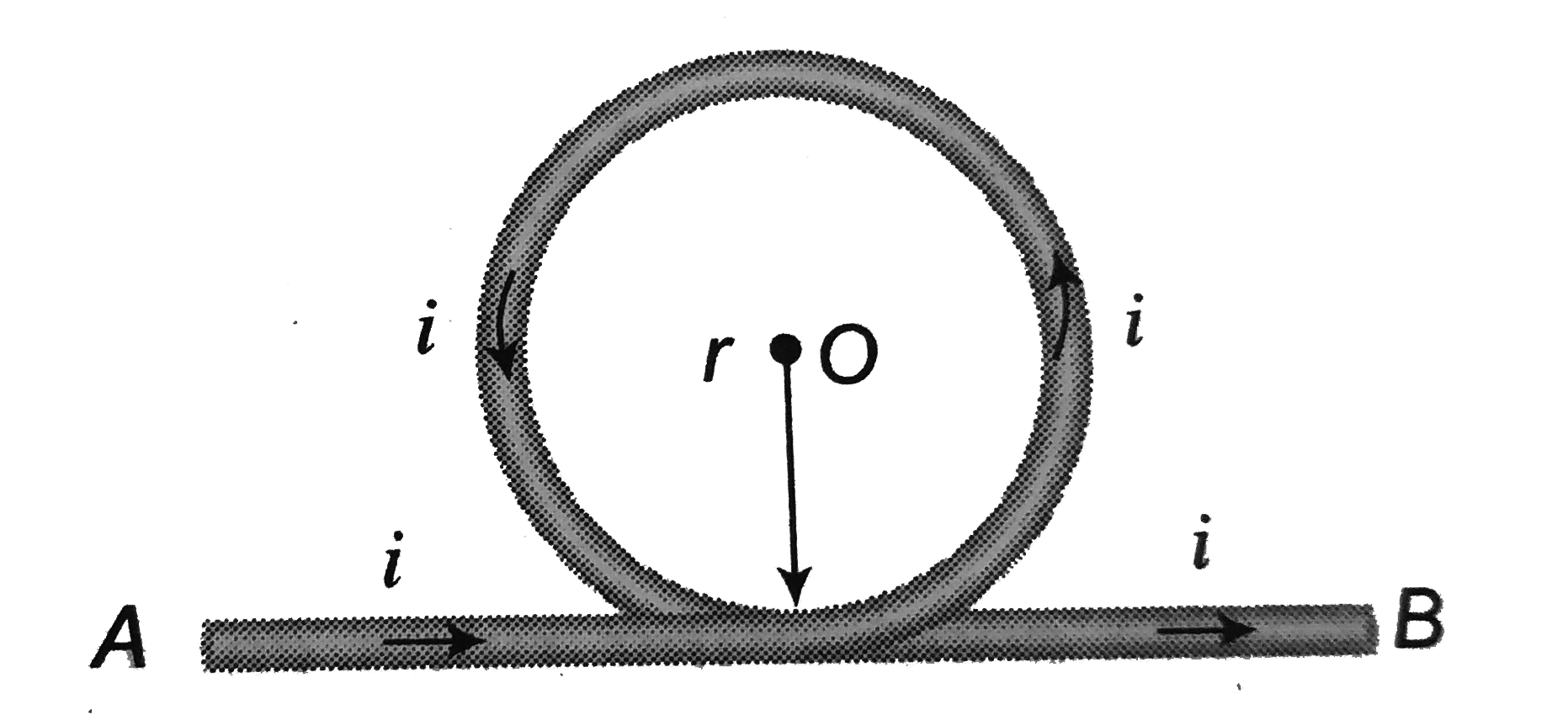
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
View SolutionA circular wire loop of radius r lies in a uniform magnetic field B, with its plane perpendicular to magnetic field. If the loop is deformed to a square shape in the same plane in time t, the emf induced in the loop is
View SolutionAn electric wire of resistance R carries a current I. When a magnetic field is applied perpendicular to the wire, the
View SolutionAn electric wire of resistance R carries a current I. When a magnetic field is applied perpendicular to the wire, the
View Solution
