A capacitor of capacitance 5μF is charged to a potential difference 200 V and then allowed to dischage through a resistance 1kΩ. The cahrge on the capacitor at the instant the current through the resistance is 100 Ma, is (in μC):
50
100
500
1000
The correct Answer is:C
To solve the problem step by step, we will follow these instructions:
Step 1: Calculate the initial charge on the capacitor
The charge Q on a capacitor is given by the formula:
Q=C×V
where:
- C is the capacitance in farads,
- V is the voltage in volts.
Given:
- C=5μF=5×10−6F
- V=200V
Substituting the values:
Q=5×10−6F×200V=1×10−3C=1000μC
Step 2: Use the current to find the voltage across the resistor
The current I through the resistor is given as 100mA=100×10−3A.
Using Ohm's Law:
VR=I×R
where:
- R=1kΩ=1000Ω
Substituting the values:
VR=100×10−3A×1000Ω=100V
Step 3: Determine the voltage across the capacitor at the moment the current is 100 mA
Since the capacitor discharges through the resistor, the voltage across the capacitor VC at that moment is equal to the voltage across the resistor:
VC=VR=100V
Step 4: Calculate the charge on the capacitor at that moment
Using the charge formula again:
Q=C×VC
Substituting the values:
Q=5×10−6F×100V=5×10−4C=500μC
Final Answer
The charge on the capacitor at the instant the current through the resistance is 100mA is:
500μC
The charge Q on a capacitor is given by the formula:
Q=C×V
where:
- C is the capacitance in farads,
- V is the voltage in volts.
- C=5μF=5×10−6F
- V=200V
Q=5×10−6F×200V=1×10−3C=1000μC
The current I through the resistor is given as 100mA=100×10−3A.
VR=I×R
where:
- R=1kΩ=1000Ω
VR=100×10−3A×1000Ω=100V
Since the capacitor discharges through the resistor, the voltage across the capacitor VC at that moment is equal to the voltage across the resistor:
VC=VR=100V
Using the charge formula again:
Q=C×VC
Substituting the values:
Q=5×10−6F×100V=5×10−4C=500μC
The charge on the capacitor at the instant the current through the resistance is 100mA is:
500μC
Similar Questions
A capacitor of capacitance 2μF is connected in a circuit as shown. Both cells have emf 2.5V and internal resistance 0.5Ω. Find the charge on capacitor (in μC )
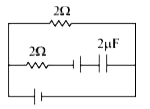
View SolutionA capacitor of capacitance 0.5μF is discharged through a resistance. Find the value of resistance if half the charge on capacitor escapes in one minute.
View Solution
Knowledge Check
A capacitor is charged to a certain potential and then allowed to discharge through a resistance R. The ratio of charge on the capacitor to current in the circuit
Achanges with timeBdoes not change with time and it is equal to time constant of circuitCdoes not change with time, but not equal to time constant of circuitDmay or may not change depending upon the charge given to the capacitorA capacitor of capacitance 5μF is charged to a potential difference 100V and then diconnected from the powerr supply. The minimum work needed to pull the plates of the capacitor apart so that the distance between them doubles is (in mJ).
A5B10C25D50A capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
ACVεB2CVε0CCV2esψlon0Dzero
A capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
View SolutionA capacitor of capacitance 200μF is connected to a battery through a resistance of 5kΩ at time t = 0. Charge stored in the capacitor in first second in larger than the charge stored in the next
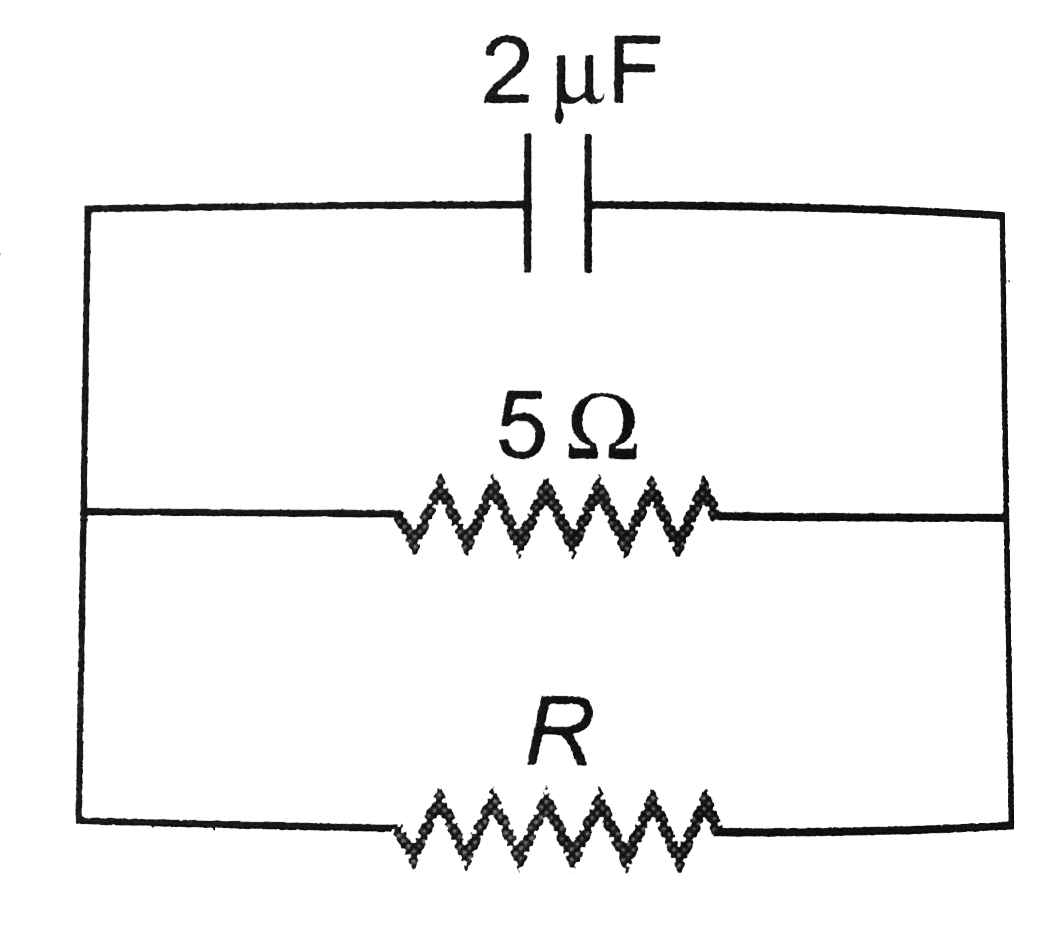
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to
View SolutionA capacitor of capacitance of 2μF is charged to a potential difference of 200V, after disconnecting from the battery, it is connected in parallel with another uncharged capacitor. The final common potential is 20V then the capacitance of second capacitor is :
View SolutionA 4μF condenser is charged to 400V and then its plates are joined through a resistance of 1KΩ. The heat produced in the resistance is :
View Solution
