Two rods are joined between fixed supports as shown in the figure. Condition for no change in the length of individual rods with the increase of temperature will be
$(α_{1}, α_{2} =$ linear expansion coefficient
$A_{1}, A_{2} =$ Area of rods
$Y_{1}, Y_{2} =$ Young modulus $)$

A

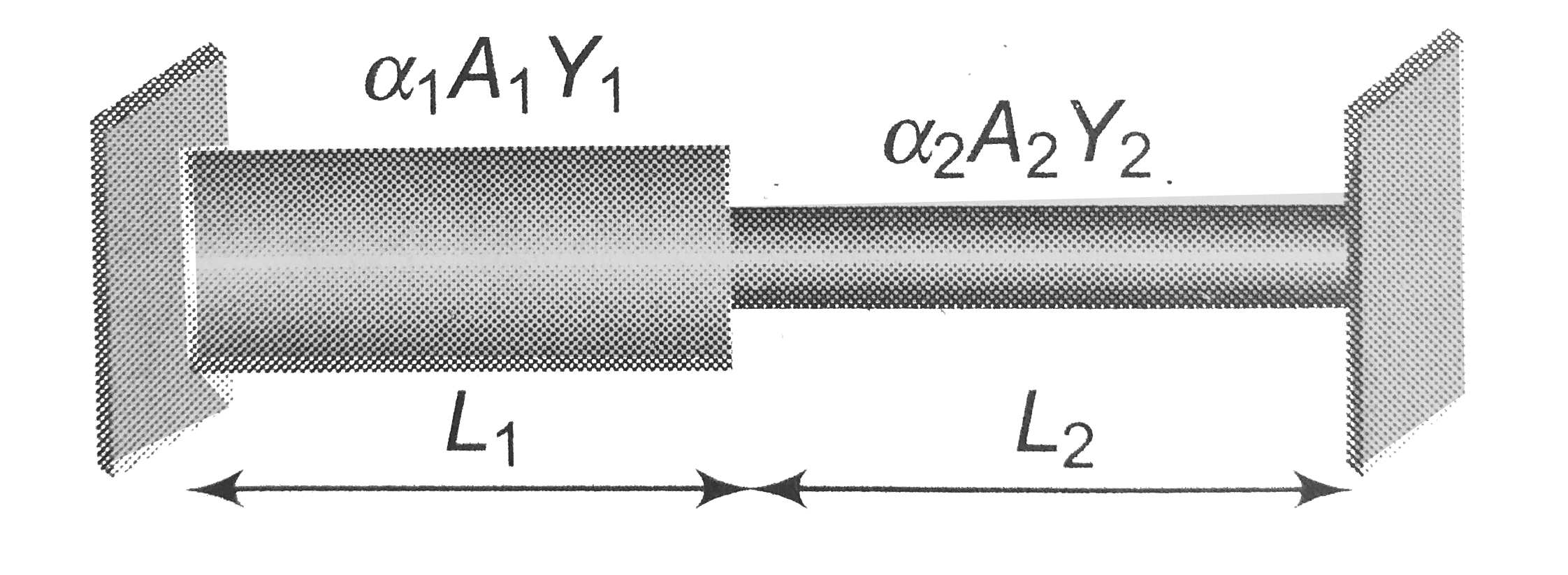
$\frac{A_{1}}{A_{2}} = \frac{α_{1} Y_{1}}{α_{2} Y_{2}}$

B

$\frac{A_{1}}{A_{2}} = \frac{L_{1} α_{1} Y_{1}}{L_{2} α_{2} Y_{2}}$

C

$\frac{A_{1}}{A_{2}} = \frac{L_{2} α_{2} Y_{2}}{L_{1} α_{1} Y_{1}}$

D

$\frac{A_{1}}{A_{2}} = \frac{α_{2} Y_{2}}{α_{1} Y_{1}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

One can take an elastic rod as a spring under elastic limits . If the temperature is increased by $Δ θ$ then $L_{1} = L_{1} (l + α_{1} Δ θ), L_{2} (l + α_{2} Δ θ)$ where $L_{1} and L_{2}$ are Natural. Length of rod at final temperature. By force balance
$K_{1} X_{1} = K_{2} X_{2} or, \frac{Y_{1} A_{1}}{L_{1}} . L_{1} α_{1} Δ θ = \frac{Y_{2} A_{2}}{L_{2}} α_{2} Δ θ or, Y_{1} A_{1} α_{1} = Y_{2} A_{2} α_{2}, \frac{A_{1}}{A_{2}} = \frac{Y_{2} α_{2}}{Y_{1} α_{1}}$

Updated on:21/07/2023

|

Class 12 PHYSICS PROPERTIES OF MATTER

Similar Questions

Knowledge Check

The variation of lengths of two moles rods $A$ and $B$ with change in temperature is shown in figure . The ratio of $\frac{α_{a}}{α_{B}}$ is :-

A $\frac{3}{2}$
B $\frac{2}{3}$
C $\frac{4}{3}$
D $\frac{3}{4}$
Two rods $A B$ and $B C$ of equal cross-sectional area are joined together and clamped between two fixed supports as shown in the figure. For the rod $A B$ and road $B C$ lengths are $l_{1}$ and $l_{2}$ coefficient of linear expansion are $α_{1}$ and $α_{2}$ , young's modulus are $Y_{1}$ and $Y_{2}$ , densities are $ρ_{1}$ and $ρ_{2}$ respectively. Now the temperature of the compound rod is increased by $θ$ . Assume of that there is no significant change in the lengths of rod due to heating. then the time taken by transverse wave pulse to travel from end $A$ to other end $C$ of the compound rod is directly proportional to

A $\sqrt{l_{2} Y_{1} + l_{1} Y_{2}}$
B $2 \sqrt{l_{2} Y_{1} + l_{1} Y_{2}}$
C $\sqrt{l_{1} Y_{2} + l_{2} Y_{1}}$
D $\sqrt{l_{2} Y_{1} - l_{1} Y_{2}}$
Two metal rods are fixed end to end between two rigid supports, as shown in figure. Each rod is of length l and area of cross-section is A. When the system is heated up, determine the condition that the junction between rode not shift. [Given $Y_{1} and Y_{2}$ are Young's modulus of materials of teh rods while $α_{1} and α_{2}$ are coefficient of linear expansion]

A $α_{1} Y_{2} = α_{2} Y_{1}$
B $α_{1} Y_{1} = α_{2} Y_{2}$
C $α_{1} = α_{2}$
D $Y_{1} = Y_{2}$

Recommended Questions

Home
Ask Doubt
Profile